Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 36
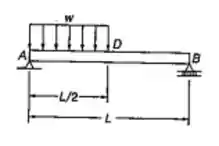
Para a viga prismática com o carregamento mostrado, determinar: a declividade no ponto ; a deflexão no ponto .
Passo 1
Fala aí galera, beleza? Vamos resolver mais um exercício de Resmat para tirar aquele 10.
Neste problema temos uma viga bi apoiada sofrendo uma carga distríbuida. Para este caso, sabemos que a declividade é dada por:
Substituindo:
E essa é a declividade, galera. Bora pra deflexão!
Passo 2
Agora, vamos calcular a deflexão no ponto , temos que utilizar a tabelinha novamente, só que dessa vez vamos procurar a equação da linha elástica. Ela é dada por:
Opa, conseguimos encontrar tudo que foi pedido. Bora fazer mais questões?
Resposta
Exercícios de Livros Relacionados
Determine a equação da linha elástica. Especifique as inclinações em A e B. EI é constante.
O feixe de molas à mesma tensão de flexão máxima em todo seu comprimento. Se a espessura das chapas de cada lâmina for t e se uma puder deslizar livremente entre a outra, mostre que o feixe de molas d
A viga cônica mostrada na figura tem largura constante b . Se ela suportar uma carga P em sua extremidade, determine a deflexão B . A carga P é aplicada a uma curta distância s da extremidade B , onde
O eixo é suportado por um mancal de apoio em A, que exerce somente reações verticais sobre o eixo, e por um mancal de encosto em B, que exerce reações horizontais, bem como reações verticais sobre o e
A haste é composta por dois eixos para os quais o momento de inércia de AB é I e de BC, 2I. Determine a inclinação e a deflexão máximas da haste devido à carga. O módulo de elasticidade é E.