Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 31

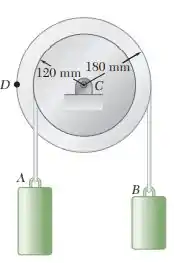
Uma polia e dois blocos estão conectados por cabos inextensíveis como mostra a figura. A polia inicia em repouso em t = 0 e é acelerada a uma taxa uniforme de 2,4   r a d / s 2 no sentido horário. Em t = 4   s , determine a velocidade e posição ( a ) do bloco A , ( b )   do bloco B .

Passo 1

Fala aí, galerinha. Tudo beleza? Bora para mais um exercício de Dinâmica. Neste problema, temos que determinar a velocidade e a posição nos pontos A   e B no instante t = 4   s .

Sabemos que a polia está num movimento uniformemente acelerado, pois ela está inicialmente em repouso e é acelerada a uma taxa uniforme. Logo, vamos utilizar a relação para este tipo de movimento, temos que a velocidade angular no instante t = 4 s é dada por:

ω = ω 0 + α t ω = 0 + 2,4 4 ω = 9,6   r a d / s 2

E para a variação angular, temos:

θ = θ 0 + ω 0 t + 1 2 α t 2 θ = 0 + 0 + 1 2 2,4 4 2 θ = 19,20   r a d

Passo 2

Agora que encontramos o deslocamento e a velocidade angular, temos que determinar a velocidade e a posição do bloco A após 4   s . Bora lá!

Podemos utilizar a relação entre o raio da polia para o carregamento A   e o momento linear. Com isso, podemos determinar a velocidade do bloco. Fica assim:

v A = r A ω v A = 0,120 9,6 v A = 1,152   m / s

E para a variação da posição do bloco, vamos relacionar o mesmo raio com o momento angular. Logo:

∆ y A = r A θ ∆ y A = 0,120 19,20 ∆ y A = 2,30   m

Opa, galera. Agora que encontramos a velocidade a o deslocamento para o carregamento A , vamos repetir o processo para o carregamento B .

Passo 3

Para o carregamento B , podemos utilizar a mesma relação anterior, entre o raio da polia   e o momento linear. Porém, para este carregamento, temos que r B = 0,180   m . Assim, podemos determinar a velocidade do bloco através da seguinte relação:

v B = r B ω v B = 0,180 9,6 v B = - 1,728   m / s

E para a variação da posição do bloco, vamos relacionar o mesmo raio com o momento angular. Logo:

∆ y B = r B θ ∆ y B = 0,180 19,20 ∆ y B = - 3,46   m

É isso, galerinha. Bora praticar mais!

Resposta

v A = 1,152   m / s

∆ y A = 2,30   m

v B = - 1,728   m / s

∆ y B = - 3,46   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera homogênea de massa me raio a é soldada a uma haste AB de massa desprezível, que é mantida por um suporte de esfera e encaixe em A. A esfera é liberada na posição β = 0 com uma taxa de prece
Dois braços em forma de L, cada um pesando 5 libras, são soldados aos pontos de um terço dos de 24 pol. deverás AB. Sabendo que o eixo AB gira a uma taxa constante ω = 180 r p m , determine (a) o mome
Um disco homogêneo de massa m = 5 kg gira a uma taxa constante ω 1 = 8 r a d / s em relação ao eixo dobrado ABC ', que por sua vez gira a uma taxa constante ω 2 = 3 r a d / s em torno de seu eixo. Det
Cada uma das placas triangulares mostradas na figura tem massa de5 kg e está soldada a um eixo vertical AB. Sabendo que o conjunto giraà taxa constante ω = 8r a d / s , determine as reações dinâmicas
Um disco homogêneo de raio ae massa é suportado por uma junta esférica em A está girando em torno de seu diâmetro vertical com uma velocidade angular constante para ω = ω 0 j quando uma obstrução é re