Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 172

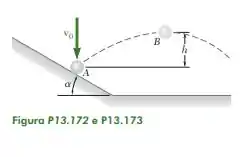
Uma esfera dá o rebote mostrado na figura após atingir um plano inclinado com uma velocidade vertical v 0 de intensidade 15   m / s . Sabendo que α = 30 ° e e = 0,8 entre a esfera e o plano, determine a altura h alcançada pela esfera.

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Pegando a direção paralela ao plano, teremos que, pela conservação de momento:

m v   s e n 3 0 ° = m v '

v ' = 7,5   m / s

Pelo coeficiente de restituição, temos que, na direção perpendicular ao chão:

- v c o s ( 30 ° ) - 0 × e = 0 - v '

v ' = 10,392   m / s

Passo 2

Agora, pegando o movimento de A   até B :

v x = v A cos ⁡ 30 ° + v A s e n 30

v x = 11,69   m / s

v y = - v ' s e n 30 ° + v ' cos ⁡ 30 °

v y = 5,24

Portanto, na direção x :

x = v x t

x = 11,69 t

Na direção y :

y = v y t - 1 2 g t 2

v y = v - g t

No ponto A :

v = 0

t = v y g

t = 0,1630 s

Achando h :

h = y

h = v t - g t 2 2

h = 5,24 × 0,16 - 16 × 0,163 2 = 0,428   m

Resposta

h = 0,428   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada uma das esferas A e B têm massa de 2k g , e estão soldadas às barras leves que estão rigidamente conectadas a um eixo como mostrado. Se o eixo é submetido a um momento de binário M = 1,5 4 t 2 +
O bloco de 5k g repousa sobre uma superfície para a qual μ k = 0,5 . Sobre ele age uma força radial de 10N e uma força horizontal de 35N , sempre direcionada a 30 ° da tangente à trajetória como mostr
O bloco de 5k g repousa sobre a superfície lisa. Sobre ele age uma força radial de 10N e uma força horizontal de 35N , sempre direcionada a 30 ° da tangente à trajetória como mostrado. Determine o tem
A bola de 1,5k g , localizada em A , é liberada do repouso e move-se para baixo sobre a trajetória curva. Se a bola exerce uma força normal de 25N sobre a trajetória quando alcança o ponto B , determi
O projétil de massa 3k g é disparado de um canhão a uma velocidade na boca do canhão v O = 500m / s . Determine a quantidade de movimento angular do projétil em relação ao ponto O no instante que ele