Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 106
Use o resultado dado para o problema e determine o módulo da projeção de sobre a linha .
Imagem do problema :
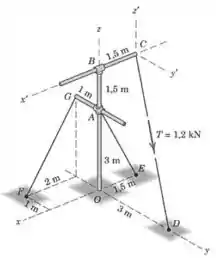
Passo 1
No problema encontramos a equação para a tração . Vamos refazer isso rapidamente. Começamos escrevendo o vetor unitário na direção de :
E então multiplicamos o módulo pelo vetor unitário:
Passo 2
Como queremos projetar esse vetor na linha , precisamos encontrar um vetor unitário nessa direção também:
E o vetor unitário nessa direção é:
Passo 3
Agora para encontrar o módulo da projeção de na direção de só precisamos fazer o seguinte produto escalar:
Resposta
A projeção de sobre a linha tem módulo .
Exercícios de Livros Relacionados
Determine a intensidade e os ângulos de direção coordenados de F 2 , de modo que a resultante das duas forças seja zero.
O poste está submetido à força F , que tem componentes atuando ao longo dos eixo x , y , z , como mostra a figura. Se a intensidade de F é 3 kN, β = 30 ° e γ = 75 ° , determine as intensidades de suas
O poste está submetido à força F , que tem componentes F x = 1,5 kN e F z = 1,25 kN. Se β = 75 ° , determine as intensidades de F e F y .
Se a força resultante que atua sobre o suporte é direcionada ao longo do eixo y positivo, determine a intensidade da força resultante e os ângulos de direção coordenados de F , de modo que β90 ° .
Se F 3 = 9k N , θ = 30 ° e ϕ = 45 ° , determine a intensidade e os ângulos de direção coordenados da força resultante que atua sobre a junta esférica