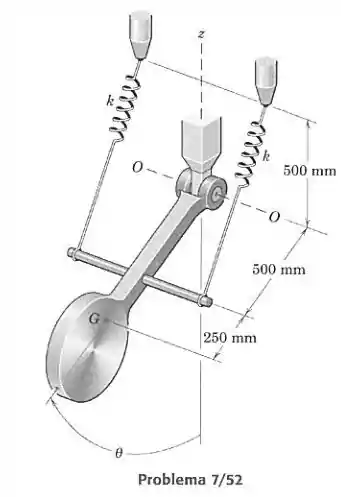
O pêndulo de 1,5 kg oscila em relação ao eixo - e tem centro de massa em . Quando , cada mola tem um alongamento inicial de 100 mm. Calcule a rigidez máxima de cada uma das molas paralelas, aqual permitirá que o pêndulo esteja em equilíbrio estável na posição inferior, em .

Primeiro vamos calcular a energia potencial devida à mola em função de . Vamos definir que . Para , o comprimento total das molas é de , e o enunciado diz que o elongamento é de . Então o comprimento da mola não alongado é:

Agora vamos calcular o tamanho total da mola para cada angulação:

Por Pitágoras, o comprimento total é:

Como :

Então o alongamento da mola é:

Passando para metros:

A diferença de energia potencial elástica entre um alongamento e outro é então:

Como :

Agora, para facilitar as contas, vamos usar uma relação trigonométrica do cosseno da metade do ângulo:

Então:

Agora calculamos a entergia potencial gravitacional do pêndulo. Vamos definir para uma altura em relação à origem igual a zero (. A altura é dada por:

Ou, colocando em metros:

Então a energia potencial gravitacional é:

Como :

A energia potencial total do sistema é então dada por:

Derivamos a expressão em relação a :

Derivando novamente:

Queremos esses valores para . Temos então:

Como mencionado no Passo 1, as condições de equilíbrio estável são:

A primeira condição já foi satisfeita. Para a segunda:

Logo, o valor máximo que pode ter é