Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 27

A porta uniforme tem massa de 20 kg e pode ser tratada como uma placa fina, tendo as dimensões mostradas na figura. Se ela está conectada a uma mola torsional em A, que tem rigidez k = 80   N . m / r a d , determine o ângulo de torção inicial da mola em radianos, necessário para que a porta tenha uma velocidade angular de 12 rad/s quando é fechada em θ = 0 ° , após ter sido aberta em θ = 90 ° , e liberada do repouso. Dica: para uma mola torsional M = k θ , onde k é a rigidez e θ é o ângulo de torção.

Passo 1

Começaremos o exercício calculando o momento de inércia da porta com relação ao seu centro de massa:

I G = 1 3 m l 2 = 1 3 20 0,8 2 → I G = 4,267   k g . m 2

Sendo assim, a energia cinética do sistema é dada por:

T = 1 2 I G ω 2

T = 1 2 4,267 ω 2

T = 2,133 ω 2

Passo 2

Como o sistema está inicialmente em repouso, T 1 = 0 . Através da analise da figura a seguir:

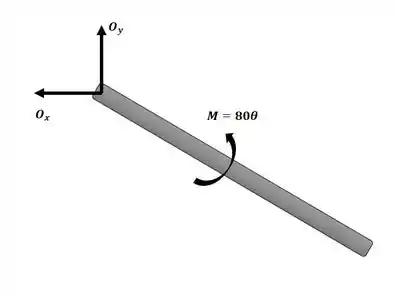
Sabemos que O x e O y não realizam trabalho, equanto M realiza.

Passo 3

Agora iremos aplicar o princípio do trabalho e da energia:

T 1 + ∑ U 1 - 2 = T 2

0 + ∫ θ O   θ O + π 2 80 θ d θ = 2,133 ω 2

40 θ O + π 2 2 - θ O 2 = 2,133 12 2

θ O = 1,66   r a d

Resposta

θ O = 1,66   r a d

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A roda é composta por um aro de 10k g enrijecido por quatro raios finos, cada um com uma massa de 2k g . Uma força horizontal de 40N é aplicada à roda inicialmente em repouso. Calcule a velocidade ang
A haste delgada de massa m e comprimento l possui uma partícula (raio desprezível, massa 2 m ) presa a sua extremidade. Se o corpo é liberado a partir do repouso quando está na posição mostrada, deter
O tronco está suspenso por dois cabos paralelos de 5m e é utilizado como um aríete. Em que ângulo θ o tronco deverá ser liberado a partir do repouso, a fim de atingir o objeto a ser esmagado com uma v
A velocidade do cilindro de 8k g é de 0,3m / s em um determinado instante. Qual é a sua velocidade v após uma queda adicional de 1,5m ? A massa do tambor com o seu encaixe é de 12k g , seu raio de gir
A placa retangular uniforme tem uma massa de 300k g e é sustentada no plano vertical pelas duas hastes paralelas de massa desprezível e pelo cabo A C . Se o cabo se rompe de repente, determine a veloc