Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 24
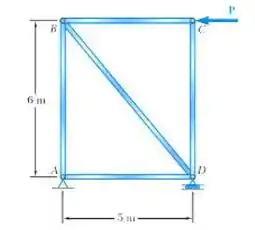
O pórtico de aço mostrado tem a escora diagonal BD com área de Determine a máxima carga P admissível se a mudança de comprimento do elemento BD não excede 1,6mm.
Passo 1
Fala aí gurizada tudo belezinha? Para determinarmos a maior carga P, então vem comigo, vamos extrair do enunciado os valores para ficar tudo bem claro, como um dia de verão!!
Calculando o comprimento L por Pitágoras temos:
Então para encontrarmos temos que usar a seguinte equação:
Passo 2
Agora temos que calcular o somatório das forcas em x, antes vamos esboçar o diagrama de corpo livre, vem comigo :D
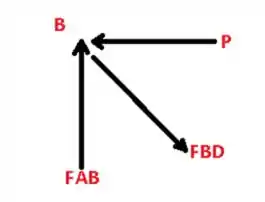
Use a articulação B como um corpo livre.
Resposta
Exercícios de Livros Relacionados
A porção cilíndrica do reservatório de ar comprimido mostrada é fabricada com chapa de 9,5 m m de espessura, soldada ao longo de uma hélice formando um ângulo β = 28 ° com a horizontal. Determinar a m
Para o tanque de armazenamento do P r o b .6.102 , determinar a máxima tensão normal e a máxima tensão de cisalhamento na parede cilíndrica, quando o tanque está completamente cheio ( h = 14,6 m )
O tanque cilíndrico de armazenamento despressurizado tem uma espessura de parede de 4,8 m m e é feito de um aço com 400M p a de tensão ultima a tração. Determine a máxima altura h de água, que pode se
Para o tanque de ar comprimido do P r o b . 6.106 , determinar a variação dos valores de β que podem ser usados, se a tensão de cisalhamento paralela à solda não deve exceder a 50M p a , quando a pres
Um torque de 8,5k N m é aplicada à extremidade de um tanque contendo óleo sob uma pressão de 2,8 M P a . Sabendo-se que o tanque tem um diâmetro externo de 250 m m e uma espessura de 6,35 m m , determ