Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 44
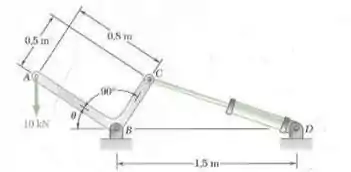
A posição da manivela ABC é controlada pelo cilindro hidráulico CD. Determine o ângulo sabendo que o cilindro hidráulico exerce uma força de no pino C.
Passo 1
Para essa questão, usaremos o mesmo principio da questão anterior, já que é o mesmo problema. Primeiramente, temos que para a altura do nosso objeto no triangulo formado por , e o solo, que:
Aplicando a lei dos cossenos para a haste CD:
Logo,
Passo 2
Temos que aplicando o trabalho virtual:
Para
Logo,
Resposta
Exercícios de Livros Relacionados
Se uma força P = 25 N é aplicada à alça do mecanismo, determine a força que o parafuso exerce sobre a rolha da garrafa. O parafuso está conectado ao pino em A e passa pelo colar que está conectado à b
Determine a força desenvolvida na mola exigida para manter a barra uniforme AB de 50 N ( ≈ 5 kg) em equilíbroo quando θ = 35º
O ‘pantógrafo de Nuremberg’ está sujeito a uma força horizontal P = 600 N. Determine a rigidez k para o equilíbrio quando θ=60º . A mola está livre quando θ=15º.
13- As conexões simétricas sustentam o cilindro de massa m no plano vertical, pela ação dos dois momentos M aplicados a O A e a O B , como mostrado. Determine o valor do momento M em função de θ . A m
14- O macaco portátil é operado por um cilindro hidráulico que controla o movimento horizontal da extremidade A do tirante, no rasgo horizontal. Determine a força compressiva C na barra do pistão do c