Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 69

Na posição mostrada na figura, a barra A B tem uma aceleração angular nula e uma velocidade angular de 20   r a d   / s no sentido anti-horário. Determine (a) a velocidade angular da barra BDH, (b) a velocidade do ponto H.

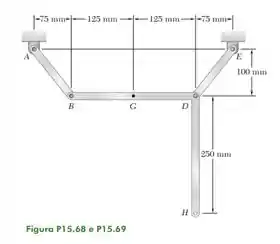
Passo 1

E aí meus caros! Missão 69 agora!

a) Bom! Primeiramente, a gente quer determinar as velocidades angulares da barra B D H !

E dessa vez, como a gente tem uma questão um pouco mais complicadinha, vamos recorrer à analise vetorial de cada barra pra tentar achar o que a gente quer!

Vamos começar pela barra A B !

Bom! Na barra A B , só vamos ter rotação, já que A está fixo!

O valor da velocidade em B , será então, de:

v B = ω A B ⋅ 0,075   m 2 + 0,100   m 2

v B = 0,125 ω A B

v B = 2,5   m / s

Passo 2

Agora, vamos analisar a parte B D H ! Aí a velocidade será dada pela soma da translação com rotação. Mais ou menos como exposto na imagem abaixo...

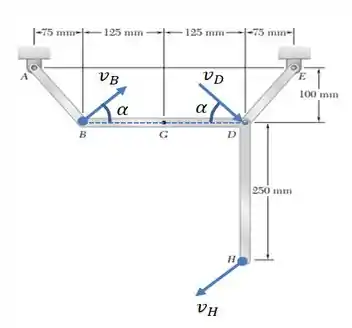
Bom! A gente tem que...

v D = v B + v D / B

Só que se reparar bem, pela configuração das barras, v D e v B são simétricos. Logo, vão ter o mesmo módulo, e a gente vai ter a seguinte situação...

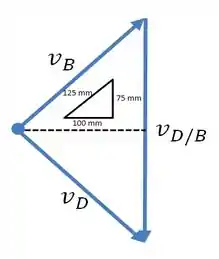
Como sabemos que v B = 2,5   m / s ; por semelhança de triângulos obtemos que...

v D / B = 2 ⋅ 75 125 ⋅ v B

v D / B = 1,2 v B

v D / B = 1,2 ⋅ 2,5

v D / B = 3   m / s

Por fim, para achar a velocidade angular de B D H , basta usar a seguinte relação, pegando o comprimento B D da barra de 250   m m :

v D / B = ω B D H ⋅ 0,25

3 = ω B D H ⋅ 0,25

ω B D H = 3,00 0,25

ω B D H = 12   r a d / s   ⤾

Passo 3

b) Em relação a velocidade v H , na barra B D H acontece a seguinte configuração de velocidades...

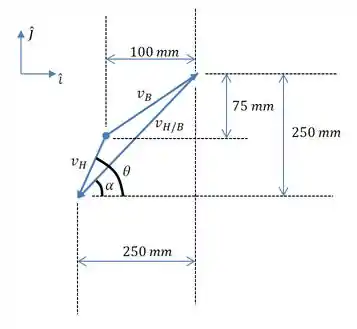
Então, primeiro calculamos v H / B , que é dada por...

v H / B = ω B D H ⋅ 0,250 2 + 0,250 2

v H / B = 3 2   m / s

E depois, podemos obter v H , através da relação vetorial...

v → H = v → B + v → H / B

Onde...

v → H = 2,0 i ^ + 1,5 j ^

v → H / B = - 3,0 i ^ - 3,0 j ^

Logo;

v → H = 2,0 i ^ + 1,5 j ^ - 3,0 i ^ - 3,0 j ^

v → H = - 1,0 i ^ - 1,5 j ^

Tirando o módulo...

v H = - 1,0 2 + - 1,5 2 ∠ tan - 1 ⁡ - 1,5 - 1,0

v H = 1,8 ∠ - 56,3 °   m / s

Resposta

a)

ω B D H = 12   r a d / s   ⤾

b)

v H = 1,8 ∠ - 56,3 °   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.59. Uma cremalheira reta repousa sobre uma engrenagem de raio r e está presa ao bloco B como mostra a figura. Representando por D a velocidade angular horária da engrenagem D e por o ângulo formado
15.60. Uma cremalheira reta repousa sobre uma engrenagem de raio r 75 mm e está presa ao bloco B como mostra a figura. Sabendo que nesse instante a velocidade angular da engrenagem D é de 15 rpm no se
15.58. No sistema biela-manivela de motor mostrado na figura, l 160 mm e b 60 mm. Sabendo que a manivela AB gira com uma velocidade angular constante de 1.000 rpm no sentido horário, determine a veloc
Nas posições mostradas nas figuras, a barra AB tem uma velocidade angular de 4r a d/ s no sentido horário. Determine as velocidades angulares das barras BD e DE.
Nas posições mostradas nas figuras, a barra AB tem uma velocidade angular de 4r a d/ s no sentido horário. Determine as velocidades angulares das barras BD e DE.