Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 89
O poste rígido e as traves cruzadas do Prob. estão mostrados novamente aqui. Determine as forças trativas e nos dois cabos de sustentação devidas à força trativa de no cabo . Considere ausência de qualquer momento de reação na base do poste em em relação aos eixos e , mas não em relação ao eixo .
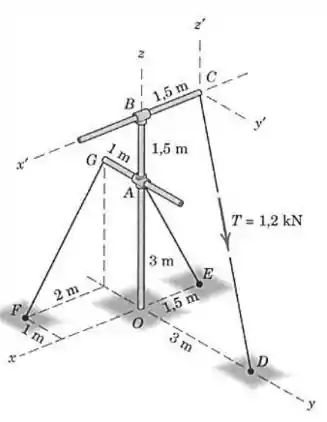
Passo 1
Como estamos lidando com três dimensões, o primeiro passo é escrever as três trações em forma vetorial.
Passo 2
Já que vamos usar o equilíbrio dos momentos para resolver essa questão, vamos escrever também os vetores posição dos pontos de aplicação de cada uma dessas forças.
A força age no ponto :
A força age no ponto :
A força age no ponto :
Beleza, agora já temos tudo para aplicar a condição de equilíbrio dos momentos.
Passo 3
Vamos somar todos os momentos em relação a origem :
E o enunciado pediu para considerarmos que pode existir um momento na origem apontando na direção de .
Vamos escrever cada um desses produtos vetoriais como o determinante de uma matriz:
E agora é só igualar cada um dos componentes resultantes dessa soma a zero, exceto a componente , que será igual a :
Vamos organizar esse sistema (e fazer algumas aproximações):
Passo 4
Nosso objetivo aqui é encontrar as forças e . Pela primeira equação do sistema temos:
E substituindo isso na segunda:
Resposta
As duas forças são e .