Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 240

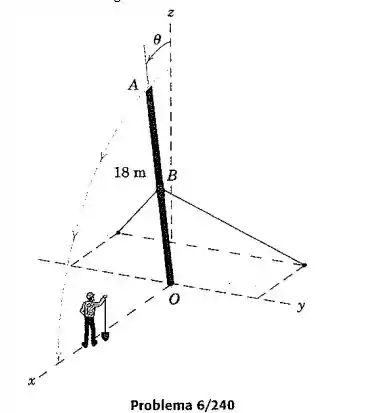
O poste telefônico de 18 m com diâmetro praticamente uniforme está sendo erguido para a posição vertical por dois cabos fixados em B , conforme mostrado. A extremidade O repousa sobre um suporte fixo e não pode deslizar. Quando o poste está quase vertical, a montagem em B inesperadamente se rompe, liberando os dois cabos. Quando o ângulo θ atinge 10º, a velocidade da extremidade superior A do poste é de 1.35 m/s. A partir desse ponto, calcule o tempo t que o operário teria para sair do caminho antes que o poste atingisse o solo. Com qual velocidade v a a extremidade A atinge o solo?

Passo 1

Para esse problema vamos usar as relações de momento fletor e de conservação de energia, como também um software para encontrar os valores da integral.

Passo 2

Vamos começar calculando o momento fletor resultante. Temos que a única forma que está sendo aplicada é a peso no centro de massa do poste. Assim, temos que o momento fletor será

∑ M o = m ⋅ g ⋅ b 2 ⋅ sin ⁡ θ = I o ⋅ θ ¨ = 1 3 ⋅ m ⋅ b 2 ⋅ θ ¨

θ ¨ = 3 2 ⋅ g b ⋅ sin ⁡ θ

Temos que para o caso translacional que d x ˙ d x = x ¨ x ˙ , pois d x ˙ d t ⋅ d t d x = x ¨ ⋅ 1 x ˙ . De maneira análoga para nosso caso, podemos dizer que:

θ ˙ ⋅ d θ ˙ = θ ¨ ⋅ d θ

Assim, podemos integrar de ambos lados da equação

∫ θ o ˙ θ ˙ θ ˙ ⋅ d θ ˙ = 3 ⋅ g 2 ⋅ b ⋅ ∫ θ o θ sin ⁡ θ ⋅ d θ

θ ˙ 2 2 - θ ˙ o 2 2 = 3 ⋅ g 2 ⋅ b ⋅ cos ⁡ θ o - cos ⁡ θ

Se manipularmos mais um pouco, ficamos com

θ ˙ = θ ˙ o 2 + 3 ⋅ g b ⋅ cos ⁡ θ o - cos ⁡ θ

E que θ ˙ = d θ d t . Assim, ficamos com

d t = d θ θ ˙ o 2 + 3 ⋅ g b ⋅ cos ⁡ θ o - cos ⁡ θ

∫ 0 t d t = ∫ θ o θ d θ θ ˙ o 2 + 3 ⋅ g b ⋅ cos ⁡ θ o - cos ⁡ θ

Usando os dados que nos é dado, θ o = 10 º = 0.1745   r a d , b = 18   m , g = 9.8   m / s 2 e θ o ˙ = v A o b = 1.35   m / s 18   m = 0.0750   r a d / s e com a ajuda de um software, temos que a solução numérica nos dá que t = 2.85   s

Passo 3

Para a velocidade quando atinge o solo, temos que é possível obter pela conservação de energia mecânica. Temos que a variação da energia tem que ser igual a zero, logo temos que

Δ T + Δ U = 0

Temos que a variação da energia cinética será

Δ T = 1 2 ⋅ I o ⋅ v a f b 2 - 1 2 ⋅ I o ⋅ v a 0 b 2 = 1 6 ⋅ m ⋅ v A f 2 - v A o 2

Para a energia potencial teremos que

Δ U = m ⋅ g ⋅ h f - m ⋅ g ⋅ h = m ⋅ g ⋅ 0 - m ⋅ g ⋅ h = - m ⋅ g ⋅ h

Δ U = - m ⋅ g ⋅ b 2 ⋅ cos ⁡ 10 º

Substituindo na equação, temos então que

1 6 ⋅ m ⋅ v A f 2 - 1.35   m / s 2 - m ⋅ 9.8   m / s 2 ⋅ 18   m 2 ⋅ cos ⁡ 10 º = 0

v A f = 1.35   m / s 2 + 6 ⋅ 4.9   m / s 2 ⋅ 18   m ⋅ cos ⁡ 10 º = 22.87   m / s

Resposta

v A f = 22.87   m / s

t = 2.85   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O borrifador de brinquedo para crianças consiste de uma coberta de 0,2k g e uma mangueira que tem massa por comprimento de 30g / m . Determine a vazão da água através do tubo de 5m m de diâmetro, de m
A curva está conectada ao cano nos flanges em A e B como mostra a figura. Se o diâmetro de cano é 0,3m e ele transmite uma descarga de 1,35m 3 / s , determine as componentes horizontal e vertical da r
O cotovelo de um cano subterrâneo de 125m m de diâmetro é submetido a uma pressão estática de 80k N / m 2 . A velocidade da água que passa por dentro dele é v = 2,4m / s . Supondo que as conexões do c
A cúpula hemisférica de massa m é mantida em equilíbrio pelo jato vertical de água descarregado por um bocal de diâmetro d . Se a descarga de água através do bocal é Q , determine a altura h a que a c
O escoadouro é usado para desviar o curso da água, Q = 0,6m 3 / s . Se a água tem uma área de seção transversal de 0,05m 2 , determine as componentes da força, no pino D e no rolete C , necessárias pa