Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.10 - Ex. 89

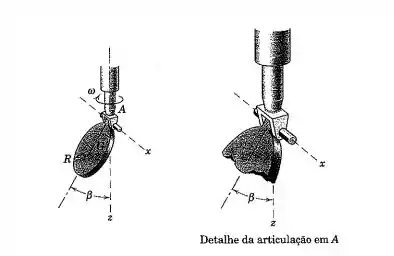
O disco circular fino de massa m e raio R é articulado em torno de seu eixo tangente horizontal à extremidade de um eixo, que gira em torno de seu eixo vertical com uma velocidade angular ω . Determine o ângulo de regime permanente β assumido pelo plano do disco com o eixo vertical. Observe qualquer limitação sobre ω para assegurar que β > 0 .

Passo 1

Para resolvermos esse problema vamos precisar usar as relações de momento fletor como também calcular a componente do momento de inércia do sistema.

Passo 2

Temos que o sistema gira em torno do eixo z , assim temos que ω = ω z e, como ω é constante, ω z ˙ = 0 . Vemos também que as forças são aplicadas na direção y e z , dessa forma temos que o momento fletor será ∑ M x = I y z ⋅ ω 2 . Precisamos então calcular o momento de inércia agora, que será dado por

I y z = ∫ y ⋅ z ⋅ d m = ∫ y o ⋅ sin ⁡ β ⋅ y o ⋅ cos ⁡ β ⋅ d m

I y z = 1 2 ⋅ sin ⁡ 2 ⋅ β ⋅ 1 4 ⋅ m ⋅ R 2 + m ⋅ R 2 = 5 8 ⋅ m ⋅ R 2 ⋅ sin ⁡ 2 ⋅ β

Dessa forma, como M x = m ⋅ g ⋅ R ⋅ sin ⁡ β . Temos que

m ⋅ g ⋅ R ⋅ sin ⁡ β = 5 8 ⋅ m ⋅ R 2 ⋅ sin ⁡ 2 ⋅ β ⋅ ω 2

Manipulando a equação, temos que β = cos - 1 ⁡ 4 ⋅ g 5 ⋅ R ⋅ ω 2 . Porém queremos que β > 0 , para isso ω 2 ≥ 4 ⋅ g 5 ⋅ R . Caso contrário, β = 0

Resposta

β = cos - 1 ⁡ 4 ⋅ g 5 ⋅ R ⋅ ω 2   p a r a   ω 2 ≥ 4 ⋅ g 5 ⋅ R

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A esfera de 20 kg rola para baixo sobre o plano inclinado sem deslizar. Determine a aceleração angular da esfera e a aceleração de seu centro de massa.
A roda de 20 kg tem um raio de giração em relação a seu centro O de k O = 300m m . Quando a roda é submetida ao momento de binário, ela desliza na medida em que rola. Determine a aceleração angular da
Dois homens exercem forças verticais constantes de 200 N e 150 N nas extremidades A e B de um pranchão uniforme que tem uma massa de 25 kg. Se o pranchão está originalmente em repouso na posição horiz
O duto de concreto circular rola com uma velocidade angular de ω = 0,5r a d / s quando o homem está na posição mostrada. Nesse instante, o centro de gravidade do duto e do homem está localizado no pon
Se um disco rola sem deslizar sobre uma superfície horizontal, mostre que quando os momentos são somados em relação ao centro instantâneo de velocidade nula, CI, é possível usar a equação de momento ∑