Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 96

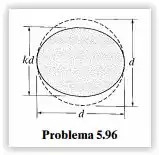
Pretende-se fabricar uma barra circular para resistir a torque; todavia, durante o processo de fabricação, a barra ficou elíptica, sendo que uma dimensão ficou menor que a outra por um fator k, como mostra a figura. Determine o fator k que causará aumento da tensão de cisalhamento máxima.

Passo 1

Ânimo! Vamos lá resolver esse exercício!

O fator que causará aumento da tensão de cisalhamento máxima é o tanto que a tensão de cisalhamento máxima na barra elíptica aumentará com relação a barra circular.

τ m á x e τ m á x c

Dados que nos foram fornecidos:

r = d 2

a = d 2

b = k d 2

Passo 2

Vamos descobrir quais são as tensões cisalhantes máximas em cada caso.

Barra circular:

τ m á x ( c ) = T c J

τ m á x c = T d 2 π 2 ⋅ d 2 4  

τ m á x c = 16 ⋅ T π ⋅ d 3  

Barra elíptica:

τ m á x ( e ) = 2 T π a b 2

τ m á x e = 2 T π ⋅ d 2 ⋅ k d 2 2

τ m á x e = 16 ⋅ T π ⋅ k 2 ⋅ d 3  

Passo 3

Agora nos resta calcular o fator de aumento:

τ m á x e τ m á x c = 16 ⋅ T π ⋅ k 2 ⋅ d 3   16 ⋅ T π ⋅ d 3  

Portanto já temos o nosso resultado:

τ m á x e τ m á x c = 1 k 2

Resposta

τ m á x e τ m á x c = 1 k 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo é feito de um material endurecido por deformação cujo diagrama τ - γ é mostrado na figura. Determine o torque T que deve ser aplicado ao eixo de modo a criar um núcleo elástico no eixo com raio
O tubo circular de aço A - 36 é submetido a um torque de 10 k N ⋅ m . Determine a tensão de cisalhamento no raio médio ρ = 60 m m e calcule o ângulo de torção do tubo se ele tiver 4 m de comprimento e
O tubo de alumínio tem 5m m de espessura e dimensões de seção transversal externa mostradas na figura. Determine a máxima tensão de cisalhamento média no tubo. Se o tubo tiver comprimento de 5m , dete
Considere um tubo de parede fina de raio médio r e espessura t . Mostre que a tensão de cisalhamento máxima no tubo devido a um torque T se aproxima da tensão de cisalhamento média calculada pela Equa
Uma escora de alumínio 2014 - T 6 está presa entre duas paredes A e B . Se tiver seção transversal quadrada de 50m m por 50m m e for submetida ao carregamento de torção mostrado, determine as reações