Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 97

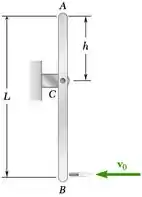
No Problema 17.96, determine (a) a distância h requerida para que a reação impulsiva em C seja nula, (b) a velocidade angular correspondente da barra imediatamente após a bala ter se alojado.

Passo 1

O enunciado pede que a gente determine a) a distância h requerida para que a reação impulsiva em C seja nula, (b) a velocidade angular correspondente da barra imediatamente após a bala ter se alojado.

Temos os seguintes dados :D

Barra:

L = 30   in. = 2.5   ft               m = 15 32.2 = 0.46584   lb ∙ s 2 /ft

I - = 1 12 m L 2 = 1 12 0.46584 2.5 2 = 0.24262   lb ∙ s 2 /ft

Bala:

m 0 = 0.08 32.2 = 0.0024845   lb ∙ s 2 /ft

Passo 2

Cinemática.

v B = L - h ω = 2.5 - h

v G = L 2 - h ω = 1.25 - h ω

Passo 3

Momentos sobre B:

0 + 0 = I - ω - m v G L 2

0 + 0 = 0.24262 ω - 0.46584 1.25 - h ω 1.25

Divide por ω

0 = 0.24262 - 0.5823 1.25 - h

Passo 4

  1. h = 0.8333   ft

    v B = 2.5 - 0.8333 ω = 1.6667 ω

    v G = 1.25 - 0.8333 ω = 0.4167 ω

    Componentes horizontais ← + :

    m 0 v 0 = m v G + m 0 v B

    0.0024845 1800 + 0 = 0.46584 0.4167 ω + 0.0024845 1.6667 ω

    Passo 5

ω = 22.56

Resposta

a )   h = 10.00   in.

b )   ω = 22.56   rad/s 

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um caixote retangular uniformemente carregado é liberado do repouso na posição mostrada na figura. Considerando que o chão é suficiente áspero para evitar o deslizamento e que o impacto de B é perfeit
Uma esfera uniforme de raio r rola para baixo sobre o plano inclinado mostrado na figura sem deslizar. Ela atinge uma superfície horizontal e, após deslizar por um momento, começa a rolar novamente. C
Uma barra delgada AB de comprimento L está em livre com uma velocidade v0 quando a corda AC se torna subitamente esticada. Considerando que o impacto é perfeitamente plástico, determine a velocidade a
Para a viga do Problema 17.117, determine a velocidade da bala de 30 g para que o ângulo máximo de rotação da viga seja de 90°.PROBLEMA 17.117 Uma bala de 30 g é disparada com uma velocidade horizonta
Um bloco retangular uniforme mostrado na figura está se movendo ao longo de uma superfície com velocidade v - 1 quando bate em uma pequena obstrução em B. Considerando que o impacto entre o canto A e