Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 123
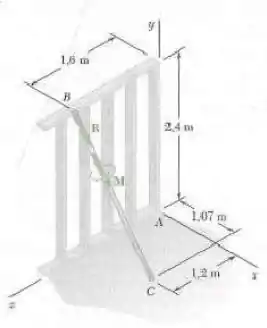
Quando um suporte ajustável é usado para aprumar uma parede, o sistema força-binário mostrado na figura é exercido sobre a parede. Substitua esse sistema força-binário por um sistema força-binário equivalente em , sabendo que e .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Para calcularmos os valores necessários, vamos criar um vetor representando a estaca. O mesmo é calculado como a diferença entre as coordenadas do ponto e as coordenadas do ponto , logo:
Passo 2
Temos então o vetor na direção da estaca. No entanto, este vetor tem comprimento diferente do valor de uma unidade.
O processo de transformação de um vetor de comprimento qualquer para um vetor unitário se chama normalização. Vamos normalizar :
Temos que:
Portanto:
Passo 3
Podemos representar vetorialmente a força e o momento agora:
E como para a força, não importa o ponto de aplicação, ela deslocada para o ponto , será a mesma coisa:
Passo 4
Para o momento, temos:
Repare no desenho, que a direção do momento é oposta a direção do vetor e por isso, usamos , com o sinal de menos no módulo do momento.
Para o cálculo do momento resultante em , precisamos calcular os vetores deslocamentos. Para cada ponto em que exista uma força aplicada, existirá um vetor deslocamento com origem em e fim no ponto de aplicação, portanto:
Obs: Podíamos escolher a distância entre qualquer ponto na linha de aplicação da força e o ponto , aqui eu escolhi a distância entre o ponto e o ponto , mas poderia por exemplo ter escolhido a distância entre o ponto e .
Agora, podemos calcular o momento resultante em , através do produtor vetorial do vetor deslocamento e das forças. Temos que:
Logo:
Resolvendo, temos:
E assim, fechamos essa!