Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 158

No projeto de uma volta completa para uma atração de um parque de diversões, deseja-se manter a mesma aceleração centrípeta ao longo de toda a volta. Assuma uma perda desprezível de energia durante o movimento e determine o raio de curvatura ρ da trajetória como função da altura y acima do ponto inferior A , onde a velocidade e o raio de curvatura são v 0 e ρ 0 , respectivamente. Para um dado valor de ρ 0 , qual é o valor mínimo de v 0 para o qual o veículo não sairá da pista na parte superior da volta?

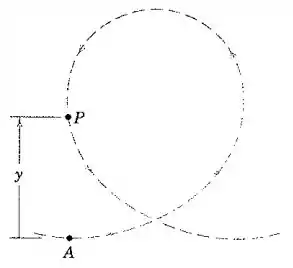
Passo 1

A conservação de energia mecânica nos dá:

Δ T + Δ V g = 0

1 2 m v 2 - v 0 2 + m g y - 0 = 0

v 2 = v 0 2 - 2 g y

Então, a aceleração centrípeta num ponto de altura y deve ser:

a n = v 2 ρ

a n = v 0 2 - 2 g y ρ

Passo 2

Porém, a gente precisa ter a aceleração centrípeta igual em todos os pontos, especificamente igual à do ponto A :

a n = v 0 2 ρ 0

v 0 2 - 2 g y ρ = v 0 2 ρ 0

Isolando ρ na equação acima, obtemos o raio de curvatura ρ como função da altura y :

ρ = v 0 2 - 2 g y v 0 2 ρ 0

Passo 3

No ponto mais alto da trajetória, temos duas forças para baixo, a normal N e o peso m g , responsáveis pela aceleração centrípeta:

m g + N = m a n

N = m a n - g

Quando o veículo perde o contato com a pista, isso significa que N = 0 . Então devemos ter N > 0 :

m a n - g > 0

a n - g > 0

v 0 2 ρ 0 - g > 0

v 0 2 ρ 0 > g

v 0 2 > ρ 0 g

v 0 > ρ 0 g

Resposta

ρ = v 0 2 - 2 g y v 0 2 ρ 0

v 0 m í n = ρ 0 g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bonde elétrico tem massa de 7500 kg e acelera ao longo de uma via reta horizontal a partir do repouso de maneira que a potência seja sempre 75 kW. Determine a distância que ele tem de se deslocar a
O motor de um carro de massa 1750 kg está gerando uma potência constante de 37,5 kW enquanto o carro está se deslocando em uma aclive com velocidde constante. Se o motor está operando com uma eficiênc
No instante mostrado, a barra de 25k g gira no sentido horário a 2r a d / s . A mola fixada em sua extremidade permanece sempre vertical, devido ao rolete guia em C . Se a mola tem um comprimento não
Resolva o Problema 18.31 usando a equação de conservação de energia.
O sistema consiste de um disco A , de 10k g , uma barra fina B C , de 2k g , e um anel liso C , de 0,5k g . Se o sico rola sem deslizar, determine a velocidade do anel no instante em que a barra torna