Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.10 - Ex. 250

O conjunto de duas esferas de 5   k g está girando livremente em torno do eixo vertical a 40   r p m com θ = 90 ° . Se a força F que mantém a determinada posição é aumentada para elevar o cursor da base e reduzir θ para 60 ° , determine a nova velocidade angular ω . Determine também o trabalho U realizado por F para mudar a configuração do sistema. Assuma que a massa dos braços e cursores é desprezível.

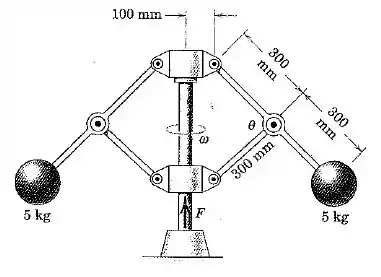
Passo 1

Bom galera, nesse exercício queremos determinar a nova velocidade angular e o trabalho realizado. Convertendo, temos

ω 0 = 40 2 π 60 = 4,19   r a d / s

Para θ = 90

r 0 = 0,1 + 2 0,3 cos ⁡ 45 = 0,524   m

Para θ = 60

r 0 = 0,1 + 2 0,3 cos ⁡ 30 = 0,62   m

Passo 2

Sabemos que

Δ H = 0

Portanto, podemos escrever

2 m r 0 2 ω 0 - 2 m r 2 ω = 0

Isolando ω e substituindo os valores, temos

ω = 0,524   0,62 2 4,19 = 3   r a d / s

Passo 3

Pela conservação da energia

U = Δ T + Δ U g

U = 2 1 2 m r 2 ω 2 - r 0 2 ω 0 2 + 2 m g 2 0,3 sin ⁡ 45 - sin ⁡ 30

Substituindo os valores, chegamos em

U = 5,34   J

Resposta

ω = 3   r a d / s

U = 5,34   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A roda de 60 kg tem um raio de giração em relação a seu centro O de k O = 300m m . Se ela é submetida a um momento de binário M = 3 t 2N . m , onde t é dado em segundos, determine a velocidade angular
Se a barra OA de massa desprezível é submetida ao momento de binário M = 9 N.m, determine a velocidade angular da engrenagem interior de 10 kg para t = 5 s após ela partir do repouso. A engrenagem tem
O carretel tem um peso de 750 N e um raio de giração em relação a seu centro de gravidade k G = 0,375m . Se ele é submetido a um torque M = 37,5 N.m e parte do repouso quando o torque é aplicado, dete
Mostre que, se uma placa está girando em torno de um eixo fixo perpendicular à placa e passando pelo seu centro de massa G, a quantidade de movimento angular é a mesma quando calculada em relação a qu
Em um dado instante, o corpo tem uma quantidade de movimento linar L = m v G e uma quantidade de movimento angular H G = I G ω calculados em relação a seu centro de massa. Mostre que a quantidade de m