Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 131
Determine a aceleração angular da barra AB e a aceleração linear de A para nessa posição. Desenvolva sua solução usando notação vetorial.
Passo 1
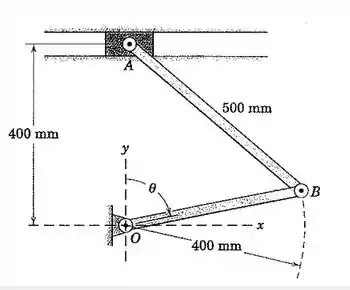
Primeiramente, vamos representar o mecanismo nas condições apresentadas pelo enunciado:
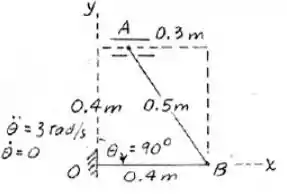
Agora, podemos calcular a velocidade e aceleração no ponto coincidente B, com base na barra OB:
Passo 2
Vamos relacionar os dados calculados do ponto B com a barra AB, através da equação da aceleração relativa:
Como não há velocidade angular, o termo normal é nulo. Portanto:
Decompondo nas direções i e j:
Resolvendo o sistema, temos que:
Resposta
Exercícios de Livros Relacionados
O movimento do cilindro de 75 mm de raio é controlado pela corda mostrada na figura. Sabendo que a extremidade E da corda tem velocidade de 300 mm/s e aceleração de 480 mm/s², ambas orientadas para ci
A barra BDE está presa a duas hastes AB e CD. Sabendo que, no instante mostrado na figura, a haste AB gira com uma velocidade angular constante de 3 rad/s no sentido horário, determine a aceleração (a
15.140. O disco de acionamento do mecanismo de cruzeta escocesa mostrado na figura tem uma velocidade angular ω e uma aceleração angular α , ambas no sentido anti-horário. Usando o método da Seção 15.
15.137. Representando por rA o vetor de posição do ponto A de uma placa rígida que está em movimento plano, mostre que (a) o vetor de posição rC do centro instantâneo de rotação é r C = r A + ω × v A
15.139. As rodas fixadas às extremidades da barra AB rolam ao longo das superfícies mostradas na figura. Usando o método da Seção 15.9 e sabendo que a aceleração da roda B é zero, deduza uma expressão