Enunciado
Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 3i
Reduza as forças representadas na figura anterior a origem dos sistemas cartesianos indicados. Idem para as forças distribuídas mostradas na figura que se segue
Passo 1
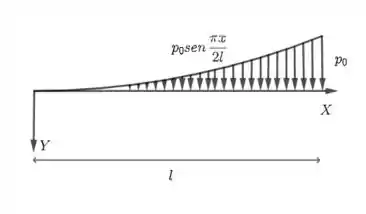
Para reduzir as forças representadas na figura, temos que notar que essas forças são paralelas e coplanares (estão todas contidas em um mesmo plano). Além disso, a força está distribuída em uma linha no plano , de modo que a resultante da força é dada por
.
No nosso caso, . Assim, para reduzir as forças, temos que resolver a integral
.
Passo 2
Se fizemos a substituição de variáveis , então . Ou seja, . Além disso, não podemos esquecer de mudar os intervalos de integração: quando , e quando , . Assim, ficamos com
Além disso, a força aponta no sentido positivo de , então .
Passo 3
Para que a força encontrada no passo anterior tenha o mesmo efeito que a força distribuída, devemos aplicá-la num ponto dado por
.
Felizmente já temos a integral do denominador. A integral do numerador é dada por
Fazendo a mesma mudança de variáveis que anteriormente, encontramos
Para não ficar muito confuso, vamos resolver a integral separadamente usando integração por partes.
.
Agora que sabemos que o resultado da integral é um, podemos concluir que . Logo, para reduzir as forças representadas na figura, temos que aplicar uma força de módulo no ponto
= .
Resposta
Para reduzir as forças representadas na figura, temos que aplicar uma força de módulo no ponto .