Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 223

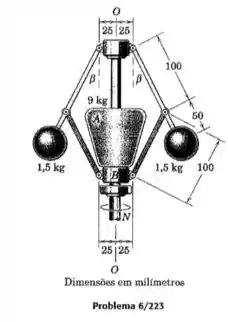
O regulador mecânico de esferas opera com um eixo vertical O - O . Quando a velocidade no eixo N é aumentada, o raio de rotação das duas esferas de 1,5 kg tende a aumentar, e a massa A de 0 kg é elevada pelo anel B . Determine o valor de em regime permanente para uma velocidade de rotação de 150 rpm. Despreze a massa dos braços e do anel.

Passo 1

Precisamos introduzir o conceito de trabalho virtual para resolver esse problema, já que ele está em regime permanente. A equação da energia cinética para um deslocamento virtual de cada uma das bolas é:

δ T = 2 m a r δ r

Onde r será:

r = 25 m m + ( 100 m m + 50 m m ) s e n β

δ r = δ 25 m m + 100 m m + 50 m m s e n β = 150 m m c o s β δ β

E a r :

a r = - r ω 2

Para a energia potencial gravitacional a equação para um deslocamento virtual é:

δ U g = - 2 m g δ h 1 - m A g δ h 2

Onde δ h 1 é a altura de cada bola, que é escrita como:

δ h 1 = δ 150 m m c o s β = - 150 m m s e n β δ β

E δ h 1 é a altura da massa central:

δ h 1 = δ 2 100 m m c o s β = - ( 200 m m ) s e n β δ β

Passo 2

Resolvendo cada uma das equações:

a r = - ( 25 m m + 100 m m + 50 m m s e n β ) 150 r p m × 2 π 60 s 2

δ T = - 2 ( 1.5 k g ) ( 25 m m + 150 m m s e n β ) 150 r p m × 2 π 60 s 2 150 m m c o s β δ β

δ T = - ( 1.06 s e n β + 10.6 ) c o s β δ β

δ U g = 2 ( 1.5 k g ) ( 9.81 m / s 2 ) 150 m m s e n β δ β + ( 9 k g ) ( 9.81 m / s 2 ) 200 m m s e n β δ β

δ U g = 22.07 J s e n β δ β

Passo 3

E então utilizamos a lei de conservação de energia:

δ T + δ U g = 0

- 1.06 s e n β + 10.6 c o s β δ β + 22.07 J s e n β δ β = 0

Passando um dos termos da soma para o outro lado e cortando δ β e a grandeza física J:

1.06 J s e n β + 10.6 J c o s β = 22.07 J s e n β

1.06 s e n β + 10.6 = 22.07 t g β

E resolvendo pelo método numérico de Newton:

β ≈ 22.5 °

Resposta

β ≈ 22.5 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma corda flexível inextensível de massa ρ por unidade de comprimento e comprimento igual a 1 / 4 da circunferência do tambor fixo de raio r é liberada a partir do repouso na posição horizontal tracej
As três pequenas esferas, cada uma com massa m , estão presas às hastes leves de modo a formar uma unidade rígida apoiada no plano vertical pela superfície circular lisa. A força de módulo constante P
A bola de golfe de 0,05k g é atingida pelo taco e desloca-se ao longo da trajetória mostrada. Determine a força impulsiva média que o taco transmite à bola, se o taco mantém contato com a bola durante
A bola de beisebol de 0,15k g tem uma velocidade de v = 30m / s , imediamente antes de ser atingida pelo taco. Após isso, ela desloca-se ao longo da trajetória mostrada, antes que o apanhador a pegue.
O bloco A , de 5k g , tem uma velocidade inicial de 5m / s ao descer por uma rampa lisa, após o que colide com o bloco estacionado B , de massa 8k g . Se os dois blocos acoplarem-se depois da colisão,