Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.9 - Ex. 218
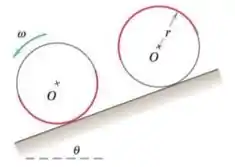
O aro circular leve de raio carrega uma tira uniforme pesada de massa em torno da metade de sua circunferência e é liberado a partir do repouso sobre a inclinação na posição superior mostrada. Após o aro rolar meia volta, (a) determine a sua velocidade angular (b encontre a força normal sob o aro se .
Passo 1
Para respondermos a letra (a), vamos primeiro considerar que o aro possui massa desprezível como é dito no enunciado e que a massa se encontra na metade da circunferência. Chamaremos de r o raio e de a posição do centro de massa, que pode ser escrita como:
Vamos precisar usar a lei de conservação de energia:
Como para o caso inicial o sistema está em repouso, sua energia cinética é zero, e para o caso final, sua energia cinética será:
E para a energia potencial, vamos colocar a posição final como nosso zero para a altura, sobrando apenas a energia potencial inicial, que será:
Como o enunciado diz que o aro rolou meia volta até a situação da letra (a), então ele rolou , e como o centro de massa está próximo à tira, quando a tira rolou meia volta com o aro, o centro de massa desceu . E as funções seno e cosseno do ângulo são as projeções dessas quantidades, já que estamos considerando apenas a altura que o aro desceu.
Ficamos então com a relação:
Passo 2
Precisamos agora encontrar o valore de , como o centro de massa não está no centro da circunferência, vamos utilizar o teorema dos eixos paralelos:
Substituindo na equação da energia cinética:
Escrevendo a velocidade do centro de massa em termos da velocidade angular:
Resolvendo:
Passo 3
Substituindo na nossa lei de conservação:
Isolando :
Resolvendo:
Passo 4
Para a letra (b), vamos utilizar a segunda lei de Newton para a coordenada y:
Como as forças que atuam no eixo y, são a força normal e a força peso:
Isolando N e reescrevendo :
Usando o que encontramos no item (a)
E para