Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 8.Problemas - Ex. 29
Um homem tenta suportar uma pilha de livros horizontalmente aplicando um força compressiva uma massa de , determine o maior número de livros que poder ser suportados na pilha. O coeficiente de atrito estático entre as mãos do homem e um livro é e entre dois livros quaisquer .
Passo 1
O problema pede que encontremos o úmero máximo de livros que pode ser colocado sem cairem.
Beleza, vamos começar fazendo calculando o peso do livro, porque o problema deu só a massa:
E a gente viu na própria questão que o coeficiente de atrito entre os livros é menor do que entre a mão e o livro, então ela é que vai ser a causa da queda dos livros.
Passo 2
Então agora vamos imaginar que a força de atrito só o que está acontecendo entre os livros, entre dois livros que a gente vai somar depois, esses livros, estão recebendo as forças diretamente, ou seja, também valem .
E a normal deles é essa mesma força, então, com ela a gente já calcula o atrito entre os livros, e fica:
Então, a gente sabe que esses vai ser responsável por segurar todos os livros que estiverem entre esses dois livros que estão em contato direto com as mãos.
Passo 3
Vamos fazer um diagrama de corpo livre agora pra ajudar, entre os livros fica:
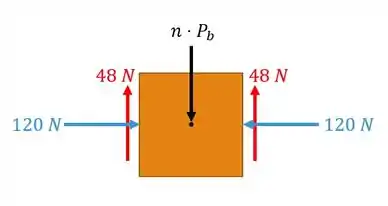
Agora fica tudo ainda mais fácil, tá vendo que as forças horizontais se anulam né? Então a gente pega somente as verticais, o peso dos livros não podem ser mais fortes que essas duas forças de atrito de , vamos lá:
Então, pode ter só até livros entre os dois livros iniciais, então o total de livros fica: