Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 33

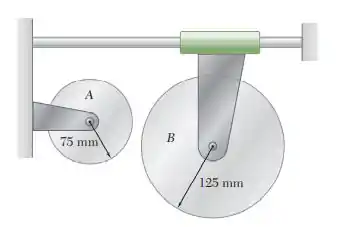
Um dispositivo simples de acionamento por atrito consiste em dois discos, A e B . Inicialmente, o disco A tem uma velocidade angular de 500   r p m e o disco B encontra-se em repouso. Sabe-se que o disco A chegará livremente ao repouso em 60   s . Entretanto, em vez de esperar até que ambos os discos estejam em repouso para pô-los em contato, uma aceleração angular constante de 2,5   r a d   / s é aplicada ao disco B no sentido anti-horário. Determine ( a ) em que instante os discos podem se postos em contato para não haver deslizamento, ( b ) a velocidade angular de cada disco quando o contato é estabelecido.

Passo 1

Fala aí, galera. Tudo certo? Bora fazer mais questões. Sabemos a velocidade angular inicial do disco A e do disco B . Logo, vamos utilizar a relação para movimento circular uniformemente variável, temos que a aceleração angular no instante t = 60   s é dada por:

ω A = ω A 0 + α A t ω A = 500   r p m + α A t 60

Vamos passar as velocidades de r p m para r a d / s . Com isso, temos:

ω A = 52,36   r a d / s + α A t 60 α A = - 0,87266   r a d / s 2

Com isso, vamos determinar este instante t em que os discos podem se postos em contato para não haver deslizamento. Vamos utilizar a mesma relação. Para A :

ω A = ω A 0 + α A t ω A = 52,36 - 0,87266 t

Para B :

α B = 2,5   r a d / s ² ω B 0 = 0

Logo:

ω B = ω B 0 + α B t ω B = 2,5 t

Passo 2

Agora, para encontrarmos a aceleração do disco B vamos usar a seguinte relação:

r A ω A = r B ω B 0,075 52,36 - 0,87266 t = 0,125 2,5 t t = 10,39   s

Passo 3

E para encontrarmos a velocidade angular de cada disco quando o contato é estabelecido vamos utilizar o instante t que encontramos no passo anterior, assim, temos que a velocidade angular de A vai ser:

ω A = 52,36 - 0,87266 t ω A = 52,36 - 0,87266 10,39 ω A = - 413   r p m

E a velocidade de B :

ω B = 2,5 t ω B = 2,5 10,39 ω B = - 248   r p m

Isso é tudo, pessoal. Bora praticar mais!

Resposta

t = 10,39   s

ω A = - 413   r p m

ω B = - 248   r p m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

18.61. Determine a taxa de variação D da quantidade de movimento angular HD do conjunto do Problema 18.1, admitindo que, no instante considerado, o conjunto tenha uma velocidade angular (12 rad /s)i e
18.64. Determine a taxa de variação G da quantidade de movimento angular HG do disco do Problema 18.4, admitindo que, no instante considerado, o conjunto tenha uma velocidade angular j e uma aceleraçã
18.65. Uma placa triangular homogênea e fina de massa de 2,5 kg está soldada a um eixo vertical leve suportado por dois mancais em A e B. Sabendo que a placa gira com uma taxa constante de 8 rad /s, d
18.66. Uma barra AB uniforme e delgada de massa m e um eixo vertical CD, cada com comprimento 2b, são soldados juntos em seus pontos médios G. Sabendo que o eixo gira numa taxa constante, determine as
Mostre que para um corpo asisimétrico sem força, a taxa de precessão pode ser expressa como ϕ ˙ = l ω 2 I ' c o s ⁡ θ onde ω 2 é o componente retangular de w ao longo do eixo de simetria do corpo.