Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 61
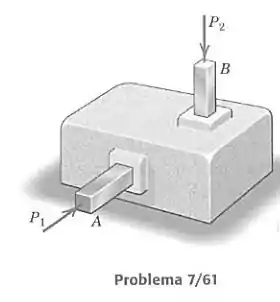
Uma “caixa preta” contém uma série de cremalheiras e pinhões, engrenagens e outros elementos mecânicos internos interconectados, os quais transformam o movimento linear da haste em um movimento linear da haste . Para cada unidade de movimento de entrada em , sob a ação da força , a barra se move para fora da caixa, um quarto de unidade, contra a ação da força . Se , calcule para haver equilíbrio. Despreze qualquer atrito e considere que todos os componentes mecânicos são corpos rígidos leves, idealmente unidos.
Passo 1
Pelo Princípio do Trabalho Virtual, o trabalho virtual todal das forças ativas para o sistema, causado num deslocamento pequeno dele deve ser zero:
Temos como forças ativas, que geram trabalho, as forças e . Vamos calcular então o trabalho virtual feito pelas duas forças para um deslocamento da haste para dentro da caixa, e então aplicar o princípio.
Passo 2
Para um deslocamento na haste entrando na haste, o tranbalho realizado por é:
O deslocamento correspondente da haste para fora da caixa será de . Como a força é para dentro e o movimento é para fora, o trabalho feito pela força é:
Passo 3
Pelo Princípio do Trabalho Virtual, então:
Como , então: