Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 40
Resolva o problema 10.39 considerando que , e . Obtenha as respostas para cada um dos seguintes quadrantes: .
Passo 1
Aplicando a ultima equação, pra determinar os valores, da questão anteriormente já respondida, temos que:
Ou,
Passo 2
Plotando isso, temos que a seguinte figura:
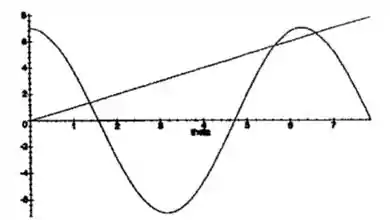
No Caso, observamos 3 pontos de intersecção. Que são as três raízes para os três quadrantes especificados na questão! Legal né?
Passo 3
Agora, basta aplicarmos aonde se encontra a reta em cada intervalo!
Resposta
Exercícios de Livros Relacionados
Determine o ângulo θ de equilíbrio, para uma dada força P . Despreze a massa das conexões.
O pedal é usado para levantar uma plataforma de massa m . Determine a força P necessária, aplicada em um ângulo de 10 ° , para suportar a carga de 80k g .
Por meio de um mecanismo de cremalheira e pinhão, grandes forças podem ser desenvolvidas pelo saca rolhas mostrado. Se o raio médio das engrenagens do pinhão vale 12m m , determine a força R que é exe
A mola de constante k não está distendida quando θ = 0 . Obtenha uma expressão para a força P necessária para defletir o sistema de um ângulo θ . A massa das barras é desprezível.
Cada uma das conexões uniformes do conjunto tem massa m e comprimento b . A posição de equilíbrio do conjunto, no plano vertical, é determinada pelo binário M , aplicado a conexão da esquerda. Express