Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.6 - Ex. 141
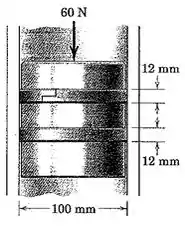
3/141) Em um teste de projeto da pressão no anel de segmento , o pistão especial de alumínio com de diâmetro com uma massa de é liberado a partir do repouso no cilindro vertical sob a ação da força constante de . O pistão atinge uma velocidade de em de curso . O coeficiente de atrito dinâmico entre os anéis de ferro fundido e o cilindro é . O diâmetro do pistão é ligeiramente menor do que o diâmetro do cilindro de modo que toda a resistência por atrito no movimento se deve ao atrito no anel de segmento . Calcule a pressão média entre os anéis e a parede do cilindro . Cada um dos dois anéis de de largura é livre para expandir em seu alojamento no pistão .
Passo 1
Então galera , para resolvermos este exercício é preciso definir que :
é a força exercidano primeiro anel .
é a força exercida no segundo anel .
Assumindo que pistão esteja em equilíbrio , temos que :
Sendo assim ,
Substituindo os valores que já conhecemos :
Passo 2
Bom pessoal , aplicando a lei de trabalho-energia , temos que :
Sendo assim ,
Isolando na equação , achamos que :
Resposta
Suave galera? Então bora próxima!!!