Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 36

Resolva o Problema 16.35, considerando que o binário M é aplicado ao disco A.

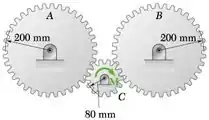
PROBLEMA 16.36 Cada uma das engrenagens A e B tem massa de 10 kg e um raio de giração de 150 mm; a engrenagem C tem uma massa de 2,5 kg e um raio de giração de 60 mm. Se o binário M de intensidade constante 6 N · m é aplicada à engrenagem C, determine (a) a aceleração angular da engrenagem A, (b) a força tangencial que a engrenagem C exerce na engrenagem A.

Passo 1

O exercício pede que a gente encontre a aceleração angular da engrenagem A, (b) a força tangencial que a engrenagem C exerce na engrenagem A.

Cinemática:

α A = α A

α A = α A

α B = α B

Passo 2

No ponto de contato entre as engrenagens A e C,

a r = r A α A = r C α C

α C = r A r C α A = 10 4 α A

Passo 3

No ponto de contato entre as engrenagens B e C,

a r = r B α B = r C α C

α B = r C r A α C = 4 10 ∙ 10 4 d A = α A

Passo 4

Cinética:

Engrenagem B:

+ Σ M B = Σ M B eff :               F B C r B = I B α B = I B α A

F B C = I B r B α A

Engrenagem C:

+ Σ M C = Σ M C eff :               F B C r C = F A B r C = I C α C

r C r B I B α A + F A B r C = 10 4 I C α C

F A C = 1 r C 4 10 I B + 10 4 I C α A

Engrenagem A:

* Σ M A = Σ M A eff :             M A - r A F A B = I A α A

M A - r A r C 4 10 I B + 10 4 I C α A = I A α A

M A = I A + I B + 10 4 2 I C α A

Passo 5

Dados:

W A = W B = 20   lb

k A = k B = 7.5   in.

= 0.625   ft

I A = I B = W A g k A 2 = 20 32.2 0.625 2

= 0.24262   lb ∙ s 2 ∙ ft

W C = 5   lb

k C = 3   in .   = 0.25   ft

I C = 5 32.2 0.25 2 = 0.009705   lb ∙ s 2 ∙ ft

M A = 50   lb ∙ in . = 4.16667   lb ∙ ft

4.1667 = 0.24262 + 0.26242 + 10 4 2 0.009705 α A

Passo 6

  1. Aceleração angular.

    2. α A = 7.6325   rad/ s 2

    Passo 7

  2. Força tangencial da engrenagem.

F A C = 1 4 12 4 10 0.24 + 10 4 0.009705 7.6325

Resposta

a )   α A = 7.63   rad/ s 2  

b )   F A C = 2.78   lb ↗

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

46. No instante que θ=30°, a manivela AB gira com uma velocidade angular e aceleração angular de ω=10rads e α=2rads2, respectivamente. Determine a velocidade e aceleração do bloco deslizante C nesse i
38. O bloco se descola para a esquerda com uma velocidade constante v 0 . Determine a velocidade angular e aceleração angular da barra como uma função de θ .
53. No instante mostrado, o disco está girando com uma velocidade angular ω e tem uma aceleração angular α . Determine a velocidade e aceleração do cilindro B nesse instante. Despreze a dimensão da po
37. O andaime S é erguido deslocando o rolete A na direção do pino em B. Se A está se aproximando de B com uma velocidade de 1,5 m/s, determine a velocidade na qual a plataforma levanta como uma funçã
45. No instante que θ = 30 ° , a manivela AB gira com uma velocidade angular e aceleração angular de ω = 10 r a d s e α = 2 r a d s 2 ,r e s p e c t i v a m e n t e . Determine a velocidade e aceleraç