Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 84
Resolva o Problema 16.64 utilizando o método do centro instantâneo de velocidade nula.
Passo 1
Precisamos começar por relembrar o problema. É importante que voltem para revisar as informações.
A questão nos dava um sistema de engrenagem planetária, cuja engrenagem R é mantida fixa, e a engrenagem mais interna é mantida girando a uma velocidade . A questão nos pede para determinar a velocidade angular das engrenagens planetárias P e do eixo A.
A análise do centro instantâneo de velocidade nos diz que:
Em que é a velocidade angular ao redor do ponto de fixação e a distância é a distância do nosso ponto fixo até o ponto de análise
Passo 2
Começaremos por determinar a velocidade do ponto de junção da engrenagem S e P. Como o centro de S está parado, temos então:
Agora que determinamos o valor desta velocidade, para podermos descobrir o valor da velocidade angular, basta olharmos a figura abaixo, a qual representa a engrenagem P.
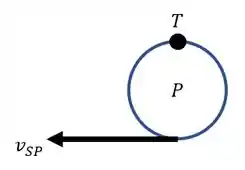
Como o ponto A tem velocidade nula (pois é um ponto de contato com a engrenagem R), temos:
Passo 3
Já para descobrirmos o valor relativo ao eixo A, precisamos descobrir antes o valor da velocidade no meio da engrenagem P. Este valor é:
Agora, o valor da velocidade angular do eixo é dado pela divisão deste valor acima pela soma dos comprimentos dos raios da engrenagem sol e da engrenagem planetária. Portanto,