Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 42
Resolva o Problema 7.20 usando o círculo de Mohr.
Passo 1
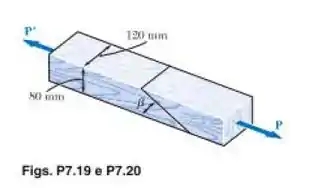
Beleza! Através dos dados que foram dados no enunciado, vamos desenhar o elemento diferencial de tensões para o estado fornecido, escrevendo em função da força P e da área da seção. Com o elemento diferencial, vamos esboçar o círculo de Mohr para o estado de tensões e encontrar o ponto para a rotação . Feito isso, conseguimos encontrar as expressões para a tensão de cisalhamento e normal nesse ponto, depois disso fica fácil! É só substituir os valores conhecidos nas expressões que encontrarmos. Então vamos lá!
Passo 2
Tá legal! Vamos começar desenhando o elemento diferencial para o estado dado, onde só temos tensão em x, então teremos:
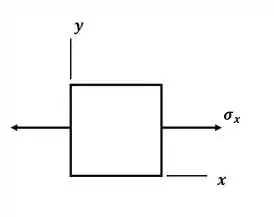
Sabemos que a tensão é dada pela força sobre a área, então, para esse elemento diferencial, temos:
Com esses valores, podemos encontrar a tensão média, dada por:
Substituindo os valores conhecidos, teremos:
Agora, vamos escrever as coordenadas dos pontos para o círculo de Mohr, no nosso caso, temos:
Então, com esses pontos, temos o seguinte círculo de Mohr:
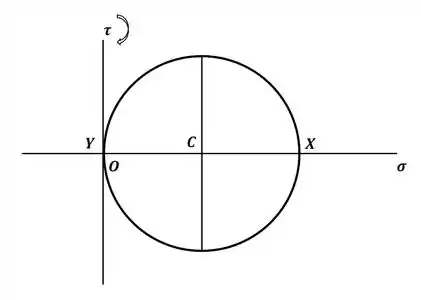
Passo 3
Com o círculo de Mohr esboçado, podemos encontrar seu raio subtraindo a tensão Y da tensão X e dividindo esse valor por 2, ou seja:
Agora precisamos rotacionar o elemento diferencial em 25° para podermos encontrar o estado de tensão na direção da junta colada. Sendo assim, rotacionando o elemento em 25°, ou seja, percorrendo 50° no círculo de Mohr, os novos pontos estarão em:
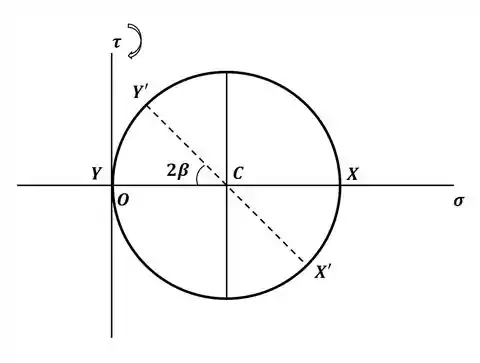
Agora precisamos encontrar as expressões para os valores da tensão normal e de cisalhamento nesse novo ponto Y’. Vamos lá! Começando pela tensão de cisalhamento pedida na letra (a), através de trigonometria, temos:
Opa! Precisamos do valor da área da seção para calcular essa tensão, então, calculando a área, temos:
Beleza! Agora é só substituir os valores conhecidos na equação para a tensão de cisalhamento, onde teremos:
A letra (a) já ficou pra trás, bora pra (b) agora!
Passo 4
Para a letra (b), precisamos da expressão para a tensão normal no ponto Y’, então, através do círculo de Mohr, temos:
Agora é só substituir os valores conhecidos, lembrando que P e foram dados no enunciado e a área é a mesma usada no passo 3, então teremos:
Feshoow! Tá aí a tensão pedida na letra (b).