Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 102
O freio de cinta simples é construído de modo que as extremidades da cinta de atrito estejam conectadas ao pino em e ao braço da alavanca em . Se a roda está sujeita a um torque de , determine a menor força aplicada à alavanca que é necessária para manter a roda parada. O coeficiente de atrito estátio entre a cinta e a roda é .
Passo 1
Analisando a roda, temos:
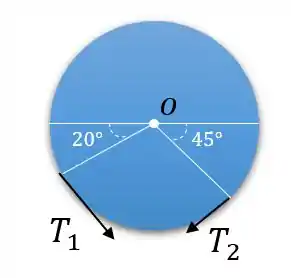
Agora vamos olhar para o atrito.
Logo,
Assim,
Passo 2
Fazendo momento com relação ao ponto O, temos:
Isto é,
Passo 3
Juantando as duas relações, temos:
Logo,
Assim,
E portanto,
Fazendo torque com relação ao ponto da figura e considernado positivo no sentido anti-horário:
Finalizando:
Resposta
Exercícios de Livros Relacionados
103. Uma corda A B C D está amarrada em dois canos, como mostra a figura. Sabendo que o coeficiente de atrito estático é 0,25 , determine (a) o maior valor da massa m para a qual o equilíbrio é possív
102. Uma corda A B C D está amarrada em dois canos, como mostra a figura. Sabendo que o coeficiente de atrito estático é 0,25 , determine (a) o menor valor da massa m para a qual o equilíbrio é possív
105. O coeficiente de atrito estático μ s entre o blocoB e a superfície horizontal e entre a corda e o suporte C é 0,40 . Sabendo que m A = 12k g , determine o menor massa do bloco B para que o equilí
104. Um bloco de 1350N é sustentado por uma corda enrolada 1 1 2 volta em torno de uma barra horizontal. Sabendo que o coeficiente de atrito estático entre a corda e a barra é 0,15 , determine a faixa
107. Uma correia plana é usada para transmitir o torque do tambor B para o tambor A . Sabendo que o coeficiente de atrito estático é 0,40 e que a tração admissível da corda é 450N , determine o maior