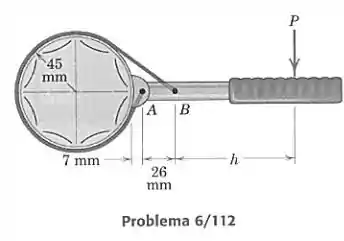
O projeto de uma chave de correia para soltar filtro de óleo está mostrado na figura. Se o coeficiente de atrito entre a correia e o filtro vale 0,25, determine o valor mínimo de que assegura que a chave não vai escorregar em torno do filtro, independentemente do módulo da força . Despreze a massa da chave e considere que o efeito da pequena peça em é equivalente àquele de uma volta de correia que começa na posição correspondente a três horas e segue no sentido horário.

Primeiro vamos definir o ângulo que a correia cobre na superfície circular.

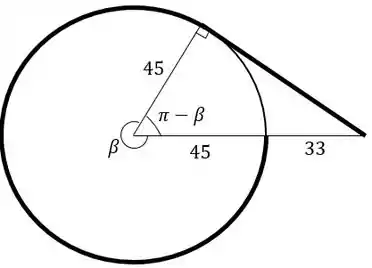
O triângulo mostrado na figura contem o ângulo suplementar a , que é ou em radianos. Pelo triângulo retângulo, calculamos o cosseno de :

Então achamos o valor de e consequentemente de :

Então aplicamos a fórmula, e descobrimos em função de :

Passando para a forma exponencial:

Agora vamos representar o cabo em diagrama de corpo livre, para fazer o momento em torno do ponto de aplicação de ser zero. Pela configuração do cabo, a tração maior deve ser pra cima, pois a diferença entre a componentes verticais de e deve ser igual a .

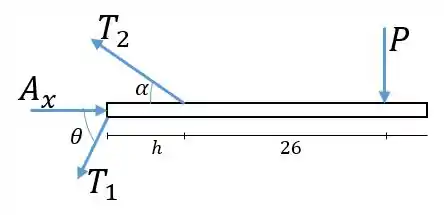
O ângulo é encontrado facilmente pelo triângulo retângulo:

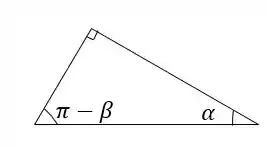
O ângulo é obtido desenhando o mesmo triângulo retângulo na parte de baixo:

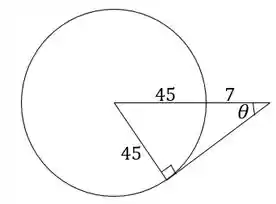
Achamos através do seno:

Ainda estamos representando os ângulos em radianos. Não precisamos do valor exato de pois só usaremos seu seno, para calcular a componente vertical de . Agora fazemos o momento em torno do ponto de aplicação de ser zero:

Substituímos por e os senos:

Agora cortamos :