Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 18

A roda e a bobina a ela fixada têm uma massa combinada de 25 kg e raio de giração em relação a seu centro k A = 150   m m . Se a polia B fixada ao motor é submetida a um torque M = 60 2 - e - 0,1 θ   N . m , onde θ está em radianos, determine a velocidade da caixa de 100 kg após ela ter se movido para cima uma distância de 1,5 m, partindo do repouso. Despreze a massa da polia B.

Passo 1

Começaremos o exercício escrevendo a velocidade linear da caixa em função da velocidade angular da bobina:

v C = ω r C = ω 0,1125

Agora iremos calcular o momento de inércia da roda A em relação ao seu centro de massa:

I A = m k A 2 = 25 0,15 2 → I A = 0,5625   k g . m 2

Sendo assim, a energia cinética do sistema é dada por:

T = T A + T C = 1 2 I A ω 2 + 1 2 m C v c 2

T = 1 2 0,5625 ω 2 + 1 2 100 ω 0,1125 2

T = 0,914 ω 2

Passo 2

Como o sistema está inicialmente em repouso, T 1 = 0 . Através da analise da figura a seguir:

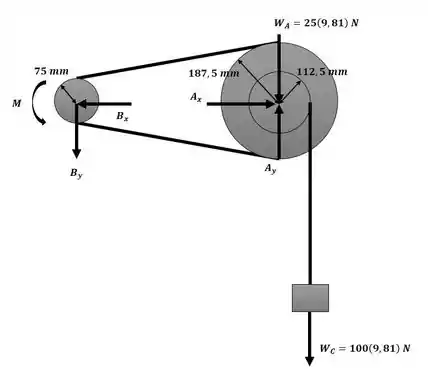
Sabemos que A x ,     A y   e W A não exercem trabalho sobre o sistema, enquanto M e W C exercem. Quando a caixa C se move 1,5 m, a roda A rotaciona de:

θ A = s C r = 1,5 0,1125 → θ A = 13,333   r a d

Sendo assim, a polia B rotaciona de um ângulo:

θ B = r A r B θ A = 0,1875 0,075 13,333 → θ B = 33,333   r a d

Sendo assim, os trabalhos realizados por M e pelo peso são dados por:

U M = ∫ M d θ B = ∫ 0 33,33 60 ( 2 - e - 0,1 θ ) d θ = 60 ( 2 θ + 10 e - 0,1 θ ) 0 33,33 → U M = 3421,39   J

U W C = - W C s C = - 100 9,81 1,5 → U W C = - 1471,5   J

Passo 3

Agora iremos aplicar o princípio do trabalho e da energia:

T 1 + ∑ U 1 - 2 = T 2

0 + 3421,39 + - 1471,5 = 0,914 ω 2

ω = 46,19   r a d / s

E substituindo esse valor na relação encontrada no passo 1:

v C = ω r C = 46,19 ( 0,1125 )

v C = 5,2   m / s

Resposta

v C = 5,2   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3/131) Umaforça horizontal constante p = 700N é aplicada ao mecanismo como mostrado . Com a esfera de 14k g inicialmente em repouso sobre seu suporte com θ = 60 ° , calcule a velocidade v da esfera qu
3/124) O terceiro estágio de um foguete lançado verticalmente para cima sobre o pólo norte sobe sem proulsão até uma altitude máxima de 500k m em seguida à queima total do combustível de seu motor . C
Calcule a velocidade horizontal v com que o carrinho de 20k g deve colidir na mola a fim de comprimi-la um máximo de 100m m . A mola é conhecida como uma mola com “endurecimento”, uma vez que sua rigi
3/130) O carro de 150k g tem uma velocidade inicial de 3 m / s para baixo do plano inclinado em A , quando uma força constante de 550N é aplicada aocabo de elevação como mostrado . Calcule a velocidad
3/128) No projeto estrutural dos andares superioresde um edifício industrial , uma tolerância deve ser dada para as quedas acidentais de máquinas pesadas através de uma pequena distância . Para uma má