Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 28
28. Determine o valor do fator de amortecimento para o sistema massa-mola-amortecedor simples apresentado.
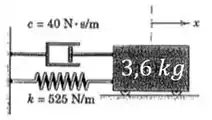
Passo 1
Bom, primeiro a gente vai calcular a frequência natural do sistema péla fórmula:
Onde é a constante elástica da mola e a massa do sistema
Passo 2
Agora, a gente vai calcular o valor do fator de amortecimento, lembrando que a sua fórmula é:
Onde é a constante do amortecedor
Resposta
O valor do fator de amortecimento será:
Exercícios de Livros Relacionados
43. A massa do sistema apresentado é liberada a partir do repouso em x 0 = 150m m , quando t = 0 . Determine o deslocamento x em t = 0,5s , se (a) c = 200N ⋅ s / m e (b) 300N ⋅ s / m .
42. A massa de um determinado sistema criticamente amortecido é liberada no instante de tempo t = 0 a partir da posição x 00 com uma velocidade inicial negativa. Determine o valor crítico ( x 0 ˙ ) c
41. O sistema apresentado é liberado a partir do repouso de uma posição inicialx 0 . Determine o deslocamento x 1 que ultrapassa a posição de equilíbrio. Assuma um movimento de translação na direção x
40. A massa de 2k g é liberada a partir do repouso a uma distância x 0 à direita da posição de equilíbrio. Determine o deslocamentox como uma função do tempo.
25. Na figura, está representado um modelo de um edifício de um andar. A barra de massa m é apoiada por duas colunas verticais elásticas leves, cujas extremidades superior e inferior estão impedidas d