Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 49
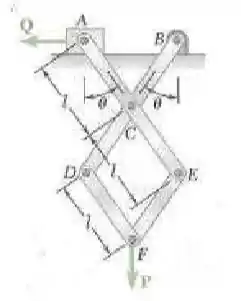
Sabendo que o coeficiente de atrito estático entre o bloco preso à barra ACE e a superfície horizontal é igual a , determine as intensidades da maior e da menor força Q para as quais o equilíbrio é mantido quando , e .
Passo 1
Usando os resultados da questão passada, já podemos jogar na formula do e !! Vamos lá!
Passo 2
Primeiro, temos que o obedece a seguinte fórmula pra esse problema:
Substituindo os valores:
Passo 3
Em seguida, temos que o nosso corresponde a:
Logo,
Resposta
e
Exercícios de Livros Relacionados
Duas hastes AC e CE são unidas por um pino em C e por uma mola AE. A constante da mola é 270 N/m, e a mola está indeformada quando θ = 30 ° . Sabendo que l = 250m m e desprezando os pesos das hastes,
Uma força vertical W é aplicada ao mecanismo articulado em B. A constante da mola é k, e a mola está indeformada quando AB e BC são horizontais. Desprezando o peso do mecanismo, deduza uma equação em
Sabendo que a constante da mola CD é k e que a mola está indeformada quando a haste ABC está horizontal, determine o valor de θ correspondente ao equilíbrio para os dados indicados. P = 300N ,l = 400m
Sabendo que a constante da mola CD é k e que a mola está deformada quando a haste ABC está horizontal, determine o valor de θ correspondente ao equilíbrio para os dados indicados. P = 300N ,l = 400m m
Determine o valor de θ correspondente para a posição de equilíbrio da haste do problema 10.12, quando l = 750m m , a = 125m m , P = 112N e Q = 180N .