Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 129

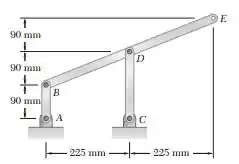
Sabendo que, no instante mostrado na figura, a barra AB tem uma velocidade angular constante de 6 rad/s no sentido horário, determine a aceleração do ponto D.

Passo 1

Vamos lá resolver mais essa. A figura abaixo mostra os sentidos das velocidades dos pontos B e D, que estão em uma mesma haste:

Assim, podemos calcular v B usando a velocidade angular de AB:

v → B = - ω A B k → × A B j → = A B ⋅ ω A B i →

v → B = 90 ⋅ 6 i → = 540 i → → v B = 540   m m / s

Vamos assumir que o centro instantâneo da barra BDE está localizado em um ponto localizado no infinito. Assim, podemos dizer que ω B D = 0 e v B = v D = 540   m m / s . Com isso, temos:

ω C D = v D C D = 540 180 = 3   r a d / s

Passo 2

Agora vamos fazer uma análise de aceleração. A aceleração angular da barra AB é nula, já que a velocidade angular é constante. Para descobrir a aceleração angular da barra BD(sentido anti-horário) vamos avaliar a aceleração de D em relação a B:

a → D = a → B + a → D / B

a → B =   - ω A B 2 A B j → = - 6 2 ⋅ 90 j → = - 3240 j →

a → D =   α C D k → × C D j → - ω C D 2 C D j → = - 180 α C D i → - 180 ⋅ 3 2 j → = - 180 α C D i → - 1620 j →

a → D / B = a → D / B t x + a → D / B t y + a → D / B n x + a → D / B n y

a → D / B = α B D k →   × 90 j → + α B D k → × 225 i → - ω B D 2 225 j → - ω B D 2 90 i → = - 90 α B D i → + 225 α B D j →

- 180 α C D i → - 1620 j → = - 3240 j → - 90 α B D i → + 225 α B D j →

Igualando os termos com as mesmas coordenadas:

- 1620 = - 3240 + 225 α B D → α B D = 7,20   r a d / s 2

- 180 α C D =   - 90 ⋅ 7,2 → α C D = 3,6   r a d / s 2

Passo 3

Agora vamos calcular a aceleração do ponto D:

a → D = - 3240 j → - 90 α B D i → + 225 α B D j →

a → D = - 3240 j → - 90 ⋅ 7,2 i → + 225 ⋅ 7,2 j →

a → D = - 648 i → - 1620 j →

a D = - 648 2 + - 1620 2 = 1745   m m / s 2

Resposta

1745 mm/s²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O centro O do disco possui a velocidade e a aceleração indicadas na figura. Se o disco rola sem deslizar sobre a superfície horizontal, determine a velocidade de A e a aceleração de B para o instante
Um carro possui uma aceleração para frente a = 4 m / s 2 sem deslizar seus pneus de 600 mm de diâmetro. Determine a velocidade v do carro quando um ponto P sobre o pneu na posição indicada terá a comp
A viga de aço de 9m está sendo levantada a partir de sua posição horizontal pelos dois cabos presos em A e B. Se as acelerações angulares iniciais dos tambores de elevação são α 1 = 0,5r a d / s 2 e α
No instante mostrado, a bola B está rolando ao longo da ranhura no disco com uma velocidade de 600mm/s e uma aceleração de 150mm/s2, ambas medidas em relação ao disco e dirigidas para longe de O. Se n
A bola C se desloca com uma velocidade de 3 m/s, que está aumentando a uma taxa constante de 1,5 m/s2, ambas medidas em relação à placa circular e direcionadas como mostrado. No mesmo instante, a plac