Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 155
Sabendo que o raio da roldana é e desprezando o atrito, determine as forças internas no ponto da estrutura mostrada na figura.
Passo 1
Bom galera, vamos fazer um diagraminha de corpo livre, só pra facilitar nossa vida:
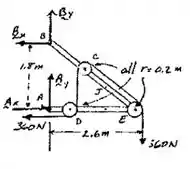
Passo 2
Show de bola, então vamos analisar o momento, com relação ao ponto que é o eixo de rotação, sabendo também que o sistema está em equilíbrio:
Resolvendo, encontramos:
Agora, o momento em relação ao ponto , como eixo de rotação:
Resolvendo também, encontramos:
Passo 3
Calma, tá quase acabando. Então a gente analisa as forças internas de :
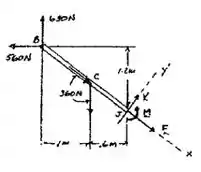
E também:
E o momento, usamos como eixo:
Resposta
Exercícios de Livros Relacionados
O guincho é usado para suspender o motor de 200k g . Determine a força que atua no cilindro hidráulico A B , as componentes horiozntal e vertical da força no pino C e as reações no apoio fixo D .
Dois cabos estão ligados em C e são carregados como mostra a figura. Determine a tração (a) no cabo A C e (b) no cabo B C .
Dois cabos estão ligados em C e são carregados como mostra a figura. Determine a tração ( a ) no cabo AC e ( b ) no cabo BC.
Dois cabos estão ligados em C e são carregados como mostra a figura. Sabendo que P = 500N e α = 60 ° , determine a tração (a) no cabo A C e (b) no cabo B C .
Dois cabos estão ligados em C e são carregados como mostra a figura. Sabendo que α = 20 ° , determine a tração (a) no cabo A C e (b) no cabo B C .