Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 154

Sabendo-se que um coeficiente de segurança de 2,8 é desejado, e usando a fórmula de Euler, determinar a maior carga P que pode ser aplicada à estrutura mostrada, quando ϑ = 30 ° .     U s a r   E = 200 G P a e considerar somente flambagem no plano da estrutura.

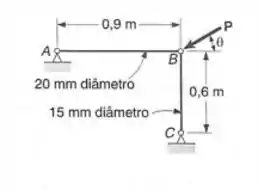
Passo 1

Partiu mais um exercício? Vamos determinar a maior carga P :D

B C :             L B C = I 2 + 0,5 2 = 1,1180 m

I = π 64 d B C 4 = π 64 20 4 = 7,854 × 10 3 m m 4 = 7,854 × 10 - 4 m 4

P e r = π 2 E I L 2 = π 2 200 × 10 9 7,854 × 10 - 9 1,1180 2 = 12,403 × 10 3 N = 12,403 k N F B , μ = P c r F . S . = 12,403 2,6 = 4,770 k N

Passo 2

AB L A B = 0 . , 5 2 + 0,5 2 = 0,70711 m

[ I = π 64 d 4 = π 64 15 4 = 2,485 × 10 3 m m 4 = 2,485 × 10 9 m 4

P c r = π 2 E I L 2 = π 2 ( 200 × 10   2,485 × 10 - 9 0,70711 2 = 9,8106 × 10 3 N = 9,8106 k N

F A B , μ = P c r F . S . = 9,8106 2,6 = 3,773 k N

Passo 3

Considere o esboço abaixo para realizarmos os somatórios das forças, vem comigo :D

+ → Σ F x = 0   0,5 0,70711 F μ - 1,0 1,1180 F B C = 0

F B C = 0,79057 F A B

+ ↑ Σ F y = 0,5 0,70711 F A B + 0,5 1,1180 F B C ← P = 0

0,70711 F A B + 0,44721 0,79057 F A B - P = 0

P = 1,06066 F A B

Passo 4

Agora sim podemos determinar a força P :D

P = 1,06066 F B C 0,79057 = 1,3416   F B C

V a l o r   p a r a   P   p e r m i t i d o

P < 1,06066   F A B , μ = 1,06066 3,773 = 4,00 k N

P < 1,3416   F B C , μ   = 1,3416 4,770 = 6,40 k N

P μ = 4,00 k N

Resposta

4,00 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em um perfil laminado de aço W 200 × 59 é usado para formar uma coluna de 7,2m de comprimento efetivo. Sabendo-se que E = 200G P a , determinar a carga centrada admissível, se o limite de escoamento d
Uma coluna de comprimento efetivo igual a 7m é obtida pela a conexão de dois perfis laminados de aço C 250× 37 , com barras de travejamento, como indicado.Sabendo-se que σ e = 250M P a e E = 200G P a
Em uma coluna é feita de metade de um perfil laminado de aço W 200× 59 ,cuja seção temas propriedades geométricas indicadas. Sabendo-se que σ e = 250M P a e E = 200G P a ,determinar a carga centrada a
Determinar a carga centrada admissível para uma coluna de 7,0 m de comprimento efetivo, que é feita do seguinte perfil laminado de aço: (a) W 310 × 143 usaremos σ e = 250M P a . Usar E = 200G P a
Uma coluna de 5,4m de comprimento efetivo é obtida pela conexão de quatro perfis laminados de aço L 76 × 76 × 9,5 , com barras de travejamento,como indicado. Sabendo-se que σ e = 250 e E = 200G P a ,