Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 177
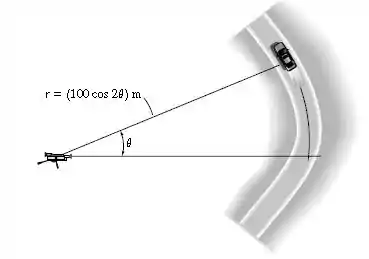
O motorista do carro mantém uma velocidade escalar constante de . Determine a velocidade angular da câmera acompanhando o carro quando .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O enunciado nos pede a velocidade angular da câmera acompanhando o carro quando . Ou seja, quando .
As intensidades são dadas por:
Nos é dada a equação da posição:
Vamos derivar essa equação dos dois lados:
Passo 2
Vamos agora aplicar :
Passo 3
Agora pensa comigo... A velocidade é tangente à trajetória, então ela forma um ângulo , como mostrado no diagrama abaixo:
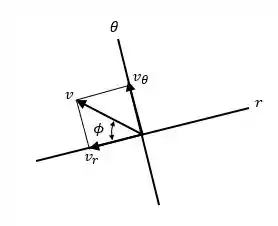
Os valores de e são então dados por:
E de acordo com o nosso diagrama, temos que:
Logo:
Dividindo as equações, temos:
Logo:
Resposta
Exercícios de Livros Relacionados
Os anéis estão conectados por um pino em B e estão livres para se mover ao longo da barra O A e da guia curvilínea O C , tendo o formato de uma cardinoide, r = 0,2 1 + cos θ m. Em θ = 30 ° , a veloc
No instante que θ = 45 ° , o atleta está correndo com uma velocidade escalar constante de 2 m/s. Determine a velocidade angular na qual a câmera deve girar a fim de seguir o movimento.
A posição de uma partícula é descrita por r = t 3 + 4 t - 4 m e θ = t 3 / 2 rad, onde t é dado em segundos. Determine as intensidades da velocidade e aceleração da partícula no instante t = 2 s.
Uma partícula move-se ao longo de uma trajetória circular de raio 300 mm. Se sua velocidade angular é θ ˙ = 2 t 2 rad/s, onde t é dado em segundo, determine a intensidade da aceleração da partícula qu
Uma partícula move-se ao longo de uma trajetória circular de raio 5 m. Se sua posição é θ = e 0,5 t rad, onde t é dado em segundos, determine a intensidade da aceleração da partícula quando θ = 90 ° .