Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 131

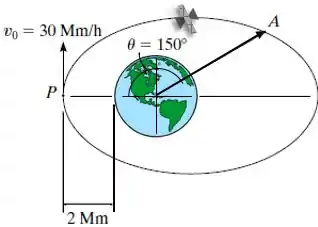
O satélite é lançado paralelo à tangente à superfície da Terra com velocidade de v 0 = 30   M m / h de uma altitude de 2 Mm acima da Terra, como mostrado. Demonstre que a órbita é elíptica e determine a velocidade vetorial do satélite quando ele chega ao ponto A .

Passo 1

O enunciado nos dá as seguintes informações:

Velocidade do satélite no ponto P : v 0 = 30   M m / h ;

Altitude do satélite no ponto P : 2   M m = 2 10 6   m .

Onde o ponto P é o seu ponto de lançamento.

Devemos demonstrar que a órbita é elíptica de determinar a velocidade vetorial do satélite no ponto A .

Suponha que o raio da Terra é 6378 km;

A massa da Terra é de M e = 5,976(1024) kg;

A massa do Sol é de M s = 1 ,99(1030) kg;

A constante gravitacional é de G = 66,73 10 - 12   m 3 / ( k g   s 2 ) .

Raio da Terra: r T = 6378   k m

Passo 2

Através da Figura, vemos que no ponto P o raio é dado por

r 0 = O P = 2 10 6 + 6378 10 3 = 8378 ( 10 3 )   m

E a velocidade em metros por segundo é igual a

v 0 = 30 10 6 m h 1     h 3600     s = 8333,33   m / s

Passo 3

Devemos saber qual a excentricidade da trajetória para determinármos se ela é elíptica.

Sabemos que

e = C h 2 G M e

Portanto, devemos encontrar os valores das constantes C e h .

Da Equação 13.20, temos que

h = r 0 v 0

logo,

h = 8378 10 3 8333,33 = 69,817 10 10   m 2 / s

Da Equação 13.21, temos que

C = 1 r 0 1 - G M e r 0 v 0 2

Logo,

C = 1 8378 ( 10 3 ) 1 - 66,73 10 - 12 5,976 ( 10 24 ) 8378 10 3 8333,33 2

C = 37,549   10 - 9   m - 1

Substituindo o valor das constante em e , obtemos

e = ( 37,549 ) ( 10 - 9 ) [ 69,817 10 10 ] 2 66,73 10 - 12 ( 5,976 ) ( 10 24 ) = 0,46

Uma trajetória elíptica ocore quando 0 < e < 1 , portanto a órbita descrita pela questão é elíptica.

Passo 4

Agora vamos determinar a velocidade no ponto A .

A Equação 13.22 nos da a equação para a trajetória de voo livre:

1 r = 1 r 0 1 - G M e r 0 v 0 2 cos ⁡ θ + G M e r 0 2 v 0 2

1 r = C cos ⁡ θ + G M e h 2

No ponto A , r = r A e θ = 150 ° . Logo,

1 r A = 1 r 0 1 - G M e r 0 v 0 2 cos ⁡ θ + G M e r 0 2 v 0 2

1 r A = 37,549 10 - 9 cos ⁡ 150 ° + 66,73 10 - 12 5,976 ( 10 24 ) 69,817 10 10 2

r A = 20,287 10 6   m

Como h é constante,

h = r A v A

v A = h r A = 69,817 10 10 20,287 10 6 = 3441,48   m / s  

v A = 3,44   k m / s

Resposta

e = 0,46

v A = 3,44   k m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro esporte está se movendo ao longo de uma trajetória inclinada cujo raio de curvatura é de ρ = 150m . Se o coeficiente de atrito estático entre os pneus e a estrada é μ s = 0,2 , determine a ve
Se uma bola de 10 kg tem velocidade de 3 m/s quando está na posição A, ao longo da trajetória vertical, determine a tração na corda e o aumento na velocidade da bola nesta posição.
A motocicleta tem massa de 0,5 Mg e dimensão desprezível. Ela passa pelo ponto A movendo-se com velocidade de 15 m/s, a qual está aumentando a uma razão constante de 1,5m / s 2 . Determine a força de
Determine a tração no arame CD logo após o arame AB ser cortado. A pequena esfera tem massa m.
O dispositivo mostrado é usado para produzir a experiência de gravidade zero em um passageiro quando ele atinge o ponto A, θ = 90 ° , ao longo da trajetória. Se o passageiro tem massa de 75 kg, determ