Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 119

O satélite está se movendo em uma órbita elíptica com uma excentricidade e = 0,25 . Determine a sua velocidade escalar quando ele está na sua distância máxima A e distância mínima B .

Passo 1

O enunciado nos deu as seguintes informações:

Excentricidade: e = 0,25 ;

Órbita elíptica.

Em seguida, nos pede para determinarmos a velocidade escalar do satélite quando ele está na sua distância máxima A e distância mínima B .

Suponha que o raio da Terra é 6378 km;

A massa da Terra é de M e = 5,976(1024) kg;

A massa do Sol é de M s = 1 ,99(1030) kg;

A constante gravitacional é de G = 66,73 10 - 12   m 3 / ( k g   s 2 ) .

Raio da Terra: r T = 6378   k m

Passo 2

A excentricidade e é dada pela seguinte fórmula:

e = C h 2 G M e

Onde, as constantes C e h são definidas por:

C = 1 r 0 1 - G M e r 0 v 0 2

h = r 0 v 0

Portanto, substituindo C e h na equação da excentricidade, temos que

e = 1 G M e r 0 1 - G M e r 0 v 0 2 r 0 v 0 2

e = r 0 v 0 2 G M e - 1

Passo 3

Sabemos o valor de e e queremos encontrar o valor da velocidade tanto no ponto B quanto no ponto A . Portanto, vamos deixar a equação da excentricidde em função de v 0 :

r 0 v 0 2 G M e = e + 1

v 0 = G M e e + 1 r 0

Passo 4

Agora vamos encontrar as velocidades pedidas.

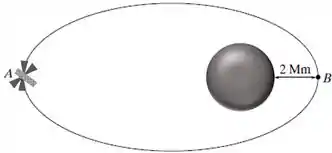
Através do desenho fornecido, vemos que o ponto B   é o mais perto, portanto é o perigeu, e o ponto A é o mais longe, sendo chamado de apogeu.

Para o ponto B :

r 0 = r p = 2 10 6 + r T

r p = 2 10 6 + 6378 10 3 = 8,378 10 6   m

v B = v 0 = 66,73 ( 10 - 12 ) ( 5,976 ) ( 10 24 ) ( 0,25 + 1 ) 8,378 10 6 = 7713   m / s

v B = v 0 = 7,71   k m / s

Para o ponto A :

r a = r 0 2 G M e r 0 v 0 - 1

r a = 8,378 ( 10 6 ) 2 ( 66,73 ) ( 10 - 12 ) ( 5,976 ) ( 10 24 ) 8,378 10 6 7713 2 - 1 = 13,96 10 6   m

Sabemos que h = r 0 v 0 = r a v a pois h é uma constante, logo

v A = r p r a v B = 8,378 10 6 13,96 10 6 7713 = 4628   m / s

v A = 4,63   k m / s

Resposta

v A = 4,63   k m / s

v B = 7,71   k m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma lata lisa de 0,75 kg é guiada ao longo da trajetória circular usando o braço-guia. Se o branço tem velocidade angular θ ˙ = 2r a d / s e a aceleração angular θ ¨ = 0 , 4r a d / s 2 no instante que
Se o coeficiente de atrito estático entre a superfície cônica e o bloco de massa m é μ s = 0,2 , determine a velocidade angular constante máxima θ ˙ sem fazer com que o bloco escorregue para cima.
Solucione o Problema 13.97 se o movimento ocorre no plano vertical.
Solucione o Problema 13.99 no instante θ = 60 ° .
Um brinquedo do parque de diversões gira com uma velocidade angular constante de θ ˙ = 0,8r a d / s . Se a trajetória do brinquedo é definida por r = ( 3 sen ⁡ θ + 5 )m e z = ( 3 cos ⁡ θ ) m , determi