Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 128

Um foguete está em órbita circular em torno da Terra a uma altitude de h = 4 Mm. Determine o incremento mínimo na velocidade escalar que ele deve ter a fim de escapar do campo gravitacional da Terra.

Passo 1

O enunciado nos diz que:

O foguete está em uma órbita circular em torno da Terra;

Altitude h = 4   M m = 4 10 6 m .

Devemos determinar o incremento mínimo de velocidade escalar para que o foguete escape do campo gravitacional da Terra

Para escapar do campo gravitacional da Terra, sua nova trajetória deve ser parabólica, conforme a ilustração abaixo.

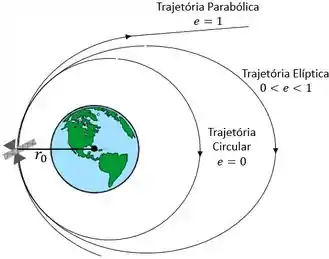
Uma trajetória parabólica possui excentricidade e = 1 e velocidade de lançamento inicial (velocidade de escape) igual a:

v e = 2 G M e r 0

Suponha que o raio da Terra é 6378 km;

A massa da Terra é de M e = 5,976(1024) kg;

A massa do Sol é de M s = 1 ,99(1030) kg;

A constante gravitacional é de G = 66,73 10 - 12   m 3 / ( k g   s 2 ) .

Raio da Terra: r T = 6378   k m

Portanto,

r 0 = h + r T = 4 10 6 + 6378 10 3 = 10,378 10 6   m

Passo 2

A velocidade escalar v c exigida para que um corpo mantenha uma trajetória circular em torno da Terra é dada pela equação 13.25:

v c = G M e r 0

v c = 66,73 ( 10 - 12 ) ( 5,976 ) ( 10 24 ) 10,378 10 6 = 6198,82   m / s

Sabemos que a velocidade de escape para uma trajetória parabólica é dada por:

v e = 2 G M e r 0

v e = 2 ( 66,73 ) ( 10 - 12 ) ( 5,976 ) ( 10 24 ) 10,378 10 6 = 8766,46   m / s

Logo, o incremento de velocidade será igual a

∆ v = v e - v c

∆ v = 8766,46   - 6198,82 = 2567,6   m / s

∆ v = 2,57   k m / s

Resposta

∆ v = 2,57   k m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola de massa m é guiada ao longo da trajetória circular vertical r = 2 r c cos ⁡ θ usando o braço O A . Se o braço tem velocidade angular constante θ ˙ 0 determine o ângulo θ ≤ 45 ° no qual a bol
Um garoto parado firmemente em pé gira a garota sentada em um ‘prato’ circular ou trenó em uma trajetória circular de raio r 0 = 3 m de tal maneira que sua velocidade angular é θ ˙ 0 = 0,1 rad/s. Se o
A partícula lisa tem massa de 80 g. Ela está ligada a uma corda elástica estendendo-se de O a P e, devido ao braço de guia ranhurado, desloca-se ao longo da trajetória circular na horizontal r = 0,8 s
O cilindro C de 1,5 kg desloca-se ao longo da trajetória descrita por r = ( 0,6 sen ⁡ θ ) m. Se o braço está girando O A no sentido anti-horário com uma velocidade angular de θ ˙ = 3 rad/s, determine
O tubo gira no plano horizontal com uma taxa constante de θ ˙ = 4r a d / s . Se a bola B de 0,2 kg parte da origem O com uma velocidade radial inicial de r ˙ = 1,5m / s e se movimenta para fora do tub