Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 183

A caixa desce deslizando pela rampa helicoidal que é definida por r = 0,5   m , θ = 0,5 t 3 r a d e z = 2 - 0,2 t 2   m , onde t é dado em segundos. Determine as intensidades da velocidade e aceleração da caixa no instante θ = 2 π   r a d .

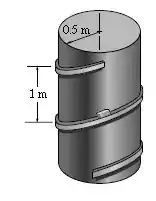
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O enunciado nos pede as intensidades da velocidade e aceleração da caixa no instante θ = 2 π   r a d .

Do enunciado, temos que:

θ = 0,5 t 3

Portanto:

2 π = 0,5 t 3

t = 2,325   s

Este é o tempo para θ = 2 π   r a d .

Queremos:

v = v r 2 + v θ 2 + v z 2

E:

a = a r 2 + a θ 2 + a z 2

Todas essas informações descobrimos derivando as equações fornecidas no enunciado:

r ˙ = d r d t

r ¨ = d r ˙ d t

θ ˙ = d θ d t

θ ¨ = d θ ˙ d t

z ˙ = d z d t

z ¨ = d z ˙ d t

Passo 2

Vamos às analises:

Como r = 0,5   m é constante, sabemos que a derivada de uma constante é zero, portanto:

r ˙ = d r d t

r ˙ = 0

E sabemos que a derivada de zero, també é zero:

r ¨ = d r ˙ d t

r ¨ = 0

Passo 3

Temos que θ = 0,5 t 3 . Aplicando t = 2,325   s , temos:

θ = 0,5 2,325 3

θ = 6,284   r a d

Temos também que:

θ ˙ = d θ d t

θ ˙ = d d t ( 0,5 t 3 )

θ ˙ = 3 ( 0,5 t 2 )

θ ˙ = 1,5 t 2

θ ˙ = 1,5 2,325 2

θ ˙ = 6,975   r a d / s 2

Logo:

θ ¨ = d θ ˙ d t

θ ¨ = d d t 1,5 t 2

θ ¨ = 2 1,5 t

θ ¨ = 3 t

θ ¨ = 3 ( 2,325 )

θ ¨ = 6,975   r a d / s 2

Passo 4

Analisando z = 2 - 0,2 t 2 e aplicando t = 2,325   s , temos:

z = z = 2 - 0,2 ( 2,325 ) 2

z = 0 , 918875   m

Então:

z ˙ = d z d t

z ˙ = d d t ( 2 - 0,2 t 2 )

z ˙ = - 2 0,2 t

z ˙ = - 0,4 t

z ˙ = - 0,4 ( 2,325 )

z ˙ = - 0,92996   m / s

Temos também que:

z ¨ = d z ˙ d t

z ¨ = d d t ( - 0,4 t )

z ¨ = - 0,4   m / s 2

Como r é constante, v r = 0 .

Passo 5

Sabemos que:

Como r é constante, v r = r ˙ = 0 .

v θ = r θ ˙

v θ = ( 0,5 ) ( 8,108 )

v θ = 4,05385   m / s

E:

v z = z ˙ = - 0,92996   m / s

A magnitude da velocidade será:

v = 0 2 + 4,05385 2 + - 0,92996 2

v = 4,16   m / s

Passo 6

Para a aceleração, teremos que a componente a r é:

a r = r ¨ - r θ ˙ 2

a r = 0 - 0,5 8,108 2

a r = - 32,867   m / s 2  

A componente a θ é dada por:

a θ = r θ ¨ + 2 r ˙ θ ˙

a θ = 0,5 6,975 + 2 ( 0 ) ( 8,108 )

a θ = 3,487   m / s 2

E a z é dada por:

a z = z ¨ = - 0,4   m / s 2

Logo:

a = - 32,867 2 + 3,487 2 + - 0,4 2

a = 33,1   m / s 2

Resposta

v = 4,16   m / s

a = 33,1   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Partindo do repouso, o garoto core para fora na direção radial a partir do centro da plataforma com uma aceleração constante de 0,5 m/s². Se a plataforma está girando com uma velocidade constante θ ˙
A fenda do braço OA gira no sentido anti-horário em torno de O com uma velociade angular constante de θ ˙ . O movimento do pino B é restrito de tal maneira que ele se move sobre a superfície circular
Um carro move-se ao longo da curva circular de raio r = 120 m com uma velocidade escalar constante de v = 9 m/s. Determine a taxa angular de rotação θ ˙ da linha radial r e a intensidade da aceleração
Se o braço OA gira no sentido anti-horário com uma velocidade angular constante de θ ˙ = 2r a d / s , determine as intensidades da velocidade e aceleração do pino P em θ = 30 ° . O pino move-se na fen
A fenda do braço OA gira no sentido anti-horário em torno de O de tal maneira que quando θ = π / 4 , o braço OA está girando com uma velocidade angular de θ ˙ e uma aceleração angular de θ ¨ . Determi