Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 172

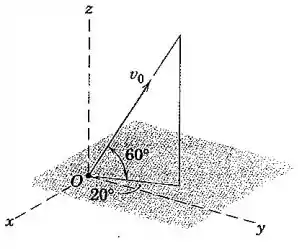
Um projétil é lançado a partir do ponto O com uma velocidade inicial de módulo v 0 = 300   m / s , direcionado como indicado na figura. Calcule as componentes x , y e z da posição, velocidade e aceleração 20 segundos após o lançamento. Despreze o arrasto aerodinâmico.

Passo 1

Galera, olhando pra figura, temos uma velocidade inicial vertical calculada assim:

v 0 z = v 0   s e n   60 ° = 300   s e n   60 ° = 259,8   m / s

E portanto, há uma velocidade horizontal de v 0 cos ⁡ 60 ° , que ainda se decompõe nos eixos x e y :

v 0 y = 300 cos ⁡ 60 ° cos ⁡ 20 ° = 140,95   m / s

v 0 x = - 300 cos ⁡ 60 °   s e n   20 ° = - 51,2   m / s

Passo 2

Para o movimento vertical, que ocorre exclusivamente no eixo z , temos aceleração constante:

a z = - g = - 9,81   m / s 2

v z = v 0 z - g t = 259,8 - 9,81 20 = 63,6   m / s

z = z 0 + v 0 z t - 1 2 g t 2 = 0 + 259,8 20 - 1 2 9,81 20 2 = 3234   m

Passo 3

Como os eixos x e y estão na horizontal, a aceleração é nula e usamos as equações de movimento uniforme:

a x = a y = 0

v x = v 0 x = - 51,2   m / s

v y = v 0 y = 140,95   m / s

x = x 0 + v x t = 0 + - 51,2 20 = - 1024   m

y = y 0 + v y t = 0 + 140,95 20 = 2819   m

Resposta

x = - 1024   m

y = 2819   m

z = 3234   m

v x = - 51,2   m / s

v y = 140,95   m / s

v z = 63,6   m / s

a x = a y = 0

a z = - 9,81   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O dispositivo robótico do Prob. 2/162 agora gira em torno de um eixo vertical fixo enquanto seu braço é prolongado e elevado. Num determinado instante, ϕ = 30 ° , ϕ ˙ = 10g r a u s / s = c o n s t a n
A haste O A é mantida no ângulo constante β = 30 ° enquanto gira em torno do eixo vertical com uma velocidade angular constante θ ˙ = 120r p m . Simultaneamente, a esfera deslizante P oscila ao longo
No projeto de uma atração de parque de diversões, os carros são ligados a braços de comprimento R que são articulados a um anel central rotativo que impulsiona o conjunto em torno do eixo vertical com
A partícula P se desloca para baixo na trajetória espiral que está enrolada ao redor da superfície de um cone circular reto com raio de base b e altura h . O ângulo γ entre a tangente à curva em qualq
A trajetória de uma partícula é definida por y ²=4 k x ² e a componente da velocidade ao longo do eixo y é V y=c t e , onde ambos os k e c são constantes. Determine as componentes x e y da aceleração