Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 181

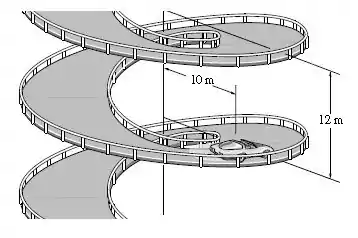
O automóvel desce da garagem de um edifício por uma rampa em espiral a uma velocidade escalar constante de v = 1,5   m / s . Se a rampa possui uma distância de 12   m para cada volta descendente completa, θ = 2 π   r a d , determine a instensidade da aceleração do carro conforme ele se desloca ao longo da rampa, r = 10   m . Dica: Para parte da solução, observe que a tangente à rampa em qualquer ponto está em um ângulo de ϕ = t g - 1 ( 12 / [ 2 π 10 ] ) = 10,81 ° com a horizontal. Use isto para determinar as componentes da velocidade v θ e v z , as quais, por sua vez, são usadas para determinar θ ˙ e z ˙ .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O enunciado nos pede a intensidade da aceleração do carro enquanto ele se desloca na rampa de raio r = 10   m .

Temos os seguintes dados:

ϕ = 10,81 °

v = 1,5   m / s

Analisando o diagrama abaixo, temos:

v θ = 1,5 cos ⁡ 10,81 °

v θ = 1,473   m / s

v z = - 1,5 sin ⁡ 10,81 °

v z = - 0,2814   m / s

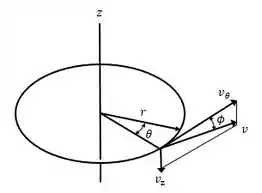
Como r é constante, v r = 0 .

Passo 2

Sabemos que:

v θ = r θ ˙

Logo:

θ ˙ = v θ r

θ ˙ = 1,473 10

θ ˙ = 0,1473   r a d / s

Quando θ = 0 , temos que:

a r = r ¨ - r θ ˙ 2

a r = 0 - 10 0,1473 2

a r = - 0,217   m / s 2

a θ = r θ ¨ + 2 r ˙ θ ˙

a θ = 10 0 + 2 ( 0 ) ( 0,1473 )

a θ = 0

a z = z ¨

a z = 0

Como:

a = a r 2 + a θ 2 + a z 2

Temos que:

a = - 0,217 2 + 0 2 + 0 2

a = 0,217   m / s 2

Resposta

a = 0,217   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro move-se ao longo de uma curva circular de raio r = 90 m. No instante mostrado, a sua taxa angular de rotação é θ ˙ = 0,4r a d / s , a qual está aumentando a uma taxa de θ ¨ = 0,2r a d / s 2 .
Uma partícula move-se ao longo de uma trajetória circular tendo um raio de 4 m, tal que sua posição como uma função do tempo é dada por θ = c o s 2 tr a d , onde t é dado em segundos. Determine a inte
Uma partícula move-se ao longo de um limaçon (ou caracol de Pascal) definido pela equação r = b - a c o s θ , onde a e b são constantes. Determine as componentes radiais e transversais da velocidade e
A posição de uma partícula é descrita por r = 300 e - 0,5 tm m e θ = 0,3 t 2r a d , onde t é dado em segundos. Determine as intensidades da velocidade e aceleração da partícula no instante t = 1,5 s.
Uma partícula move-se ao longo de uma espiral de lituus definida pela equação r 2 θ = a 2 , onde a é uma constante. Determine as componentes radiais e transversais da velocidade e aceleração da partíc