Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.5 - Ex. 117

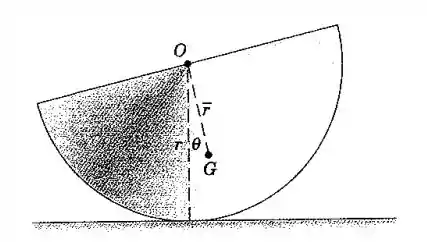
O semicilindro de massa m e raio r rola sem deslizar sobre a superfície horizontal. Por meio do método dessa seção, determine o período τ para pequenas oscilações.

Passo 1

Bom pessoal, nesta questão é importante saber a localização do centro de massa de um semicírculo. Em relação ao ponto O, temos:

r - = 4 r 3 π

Beleza! Vamos agora calcular a energia cinética.

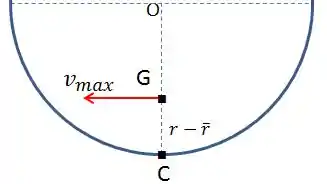
O semicilindro gira sem deslizar, portanto, o ponto de contato com o chão é o centro instantâneo de velocidade nula C, e é o ponto ao qual ele gira. Devemos então obter o momento de inércia para este ponto C, através do teorema dos eixos paralelos. Também é importante pontuar que a energia cinética é máxima quando θ = 0 .

Primeiro vamos encontrar o momento de inércia para o eixo C.

I C = I G + m d 2 = I O - m r - 2 + m r - r - 2

I C = 1 2 m r 2 + m r 2 - 2 m r r - = 3 2 - 8 3 π m r 2

Agora, substituímos na equação da energia cinética.

T = 1 2 3 2 - 8 3 π m r 2 θ ˙ 2

T = 3 4 - 4 3 π m r 2 θ ˙ 2             ( 1 )

Passo 2

Agora vamos para a parte de energia potencial.

A energia potencial do sistema é igual a variação da energia potencial gravitacional.

Veja a figura abaixo:

Quando a barra se desloca um ângulo θ para a direita, o centro de massa da massa sobe r -   ( 1 - c o s θ ) .

Podemos então escrever a equação da energia potencial:

V = m g r -   ( 1 - c o s θ )             ( 2 )

Agora, vamos voltar para a equação de energia do sistema. Basta juntar as equações (1) e (2):

E = T + V

E = 3 4 - 4 3 π m r 2 θ ˙ 2 + m g r -   ( 1 - c o s θ )

Como o sistema é conservativo, d E d t = 0 (Não esquecer a regra da cadeira):

d E d t = 3 2 - 8 3 π m r 2 θ ˙ θ ¨ + m g r -   ( θ ˙ s e n θ ) = 0

3 2 - 8 3 π r 2 θ ¨ + g 4 r 3 π s e n θ = 0

Para pequenos ângulos, usamos a aproximação s e n θ = θ :

3 2 - 8 3 π r θ ¨ + g 4 3 π   θ = 0

Ajeitando a equação:

θ ¨ + g 4 3 π 3 2 - 8 3 π r   θ = 0

θ ¨ + 8 g 9 π - 16 r   θ = 0

Agora temos uma equação nos moldes da equação do movimento harmônico. Com isto, sabemos a frequência natural:

ω n = 8 g 9 π - 16 r   = 0,807 g r     r a d / s  

Podemos relacionar o período à velocidade angular:

ω n = 2 π τ

Substituindo na equação, temos que:

τ = 2 π 0,807 r g   = 7,78 r g     s

Resposta

τ = 7,78 r g     s e g u n d o s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14.7E A) Mostre que a lagrangeana do oscilador visto na Figura 14.7 é L = 1 2 M y ' 2 - 1 2 k y 2 - M g y - y 0 , onde y 0 é o ponto de referência para a energia potencial gravitacional. B) Mostre que
14.3E Considere que o oscilador descrito em Exercicio 14.2 tenha energia de 1,00J e frequência angular de 6,28rad /s . A) Faça um gráfico de L t no intervalo de tempo 0 ≤ t ≤ 1,00s .
14.2E Considere um oscilador harmônico constituído de uma massa m forçada por uma mola de constante elástica k . As condições iniciais do oscilador são x 0 = A ,v 0 = 0 . A) Mostre que a lagrangeana d
Uma mola de massa desprezível está pendurada no teto com um pequeno objeto preso à extremidade inferior. O objeto é inicialmente mantido em repouso em uma posição y , tal que a mola se encontra no est
12 . Uma esfera de raio r e massa m , sob o efeito da gravidade, rola no interior de uma casca esférica imóvel de raio R . A ) Escreva a lagrangeana do sistema para pequenos deslocamentos da esfera em