Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 209

Para a configuração de cursor e manivela apresentada, desenvolva a expressão para a velocidade v A do pistão (admitida positiva para a direita) como função de θ . Substitua os dados numéricos do Exemplo 5/15 e calcule v A como uma função de θ para 0 ≤ θ ≤ 180 ° . Represente graficamente v A contra θ e encontre seu módulo máximo e o valor correspondente de θ . Por simetria estime os resultados para 180 ≤ θ ≤ 360 ° .

Passo 1

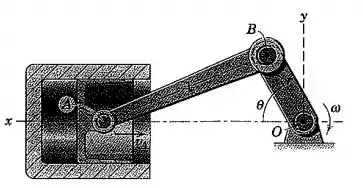
Bom pessoal, vamos representar o mecanismo para tirar algumas relações entre suas variáveis:

Podemos tirar as seguintes relações da figura:

x = l c o s β + r c o s θ         ( 1 )

l s e n β = r s e n θ                         ( 2 )

A partir da derivada da primeira equação, vamos encontrar o comportamento de x ao longo do tempo (está diminuindo o tamanho):

x ˙ = - l β ˙ s e n β - r θ ˙ s e n θ

Porém, o ponto O está fixo, então a taxa que x está diminuindo é a velocidade de A. Entretanto, o enunciado pede para considerar a velocidade para direita como positiva. Temos então que:

v A = - x ˙ =   l β ˙ s e n β + r θ ˙ s e n θ         ( 3 )    

Agora, vamos derivar a segunda equação:

l β ˙ c o s β = r θ ˙ c o s θ

β ˙ = r l θ ˙ c o s θ c o s β         ( 4 )

Podemos unir as equações (3) e (4): Veja que ( θ ˙ = ω )

v A = l r l θ ˙ c o s θ c o s β s e n β + r θ ˙ s e n θ    

v A = r ω c o s θ c o s β s e n β + r ω s e n θ       ( 5 )    

Vamos fazer algumas modificações na equação acima para ficar como o gabarito:

c o s β = 1 - s e n 2 β

Usando a equação (2):

c o s β = l r 2 - s e n 2 θ

Agora vamos substituir isso na equação (5):

v A = r ω s e n θ   1 + c o s θ l r 2 - s e n 2 θ

Passo 2

Agora o exercício pede para usar os dados do Exemplo 5/15. Vamos a eles:

r = 125 m m

l = 350 m m

ω = 1500 2 π 60 = 157,1   r a d / s

Substituindo os valores na equação:

v A = 19,63   s e n θ   1 + c o s θ 7,84 - s e n 2 θ

Agora vamos plotar o gráfico (em radianos) da expressão acima para o intervalo 0 ≤ θ ≤ π :

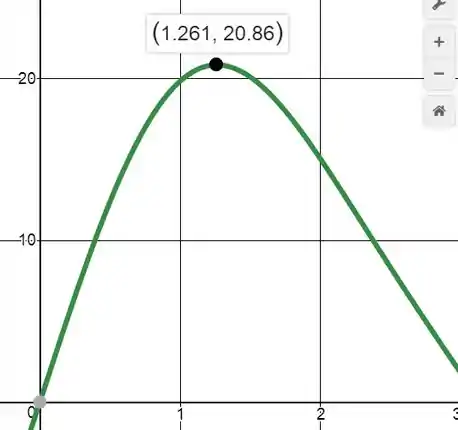
Interpretando o gráfico acima, temos que:

θ = 1,261   r a d = 72,2 °

v A = 20,86   m / s

Para o intervalo 180 ≤ θ ≤ 360 ° :

v A = - 20,86   m / s

θ = 5,022   r a d = 287,74 °

Resposta

v A = r ω s e n θ   1 + c o s θ l / r 2 - s e n 2 θ

θ = 1,261   r a d = 72,2 °

v A = 20,86   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o anel A se desloca com uma velocidade constante v A = 5 im / s , determine a velocidade do anel B quando a barra A B está na posição mostrada. Suponha que a velocidade angular de A B é perpendicul
No instante mostrado, o tubo gira em torno do eixo z com uma velocidade angular xonstante ω 1 = 2r a d / s , enquanto no mesmo instante o tubo gira para cima com uma taxaconstante de ω 2 = 5r a d / s
No instante θ = 30 ° , a estrutura do guindaste e a lança A B está girando com uma velocidade angular constante ω 1 = 1,5r a d / s e aceleração angular ω ˙ 1 = 0,5r a d / s 2 , equanto a lança A B gir
Quando a barra A B está na posição mostrada, o anel A se desloca com uma velocidade v A = 5 im / s e aceleração a A = 1 im / s 2 . Determine a aceleração do anel B nesse instante. Suponha que a veloci
No instante θ = 30 ° , a estrutura do guindaste e a lança A B giram com uma velocidade angular constante ω 1 = 1,5r a d / s e ω 2 = 0,5r a d / s , respectivamente. Determine a velocidade e a aceleraçã