Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 67
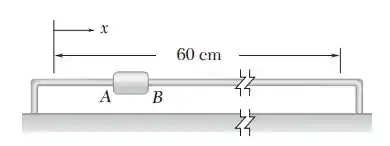
Um sensor de temperatura está acoplado ao cursor AB, que se desloca para frente e para trás ao longo de 60 cm. As velocidades máximas do cursor são 12 cm/s para a direita e 30 cm/s para a esquerda. Quando o cursor se desloca para a direita, ele acera e desacelera a uma taxa constante de 6 cm/s² quando se desloca para a esquerda, acelera e desacelera a uma taxa constante de 20 cm/s². Determine o tempo necessário para o cursor completar m ciclo inteiro e construa as curvas v-t e x-t de seu movimento.
Passo 1
E ai gurizada tudo belezinha???
A curva v-t e primeiro desenhada como mostrado. Então,
Agora
Ou
Ou
E
Ou
Ou
Agora
Passo 2
Nós temos
Em,
Resposta
a)
Exercícios de Livros Relacionados
28. Se os efeitos da resistência atmosférica são levados em consideração, um corpo caindo tem uma aceleração definida pela equação a = 9,81 1 - v 2 10 - 4 m s 2 , onde v é dado em m/s e a direção posi
41. Uma partícula está se movendo ao longo de uma linha reta de maneira que sua posição de um ponto fixo é s = 12 - 15 t 2 + 5 t 3m , onde t é dado em segundos. Determine a distancia total percorrida
26. A aceleração de uma partícula movendo-se ao longo de uma linha reta é a=0,02etms2, onde t é dado em segundos. Se v=0, s=0 quando t=0, determine a velocidade e a aceleração da partícula em s=4m.
32. A bola A é jogada verticalmente para cima do topo de um prédio de 30m com uma velocidade inicial de 5 m/s. No mesmo instante, outra bola B é jogada para cima a partir do chão com uma velocidade in
36. A aceleração de uma partícula movendo-se ao longo de uma linha reta é a = 8 - 2 sm / s 2 , onde s é dado em metros. Se v = 0e ms = 0 , determine a velocidade da partícula em s = 2m e a posição da