Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 40

No sistema biela-manivela do motor mostrado na figura, a manivela A B tem uma velocidade angular horária constante de 1,5 m / s . Para a posição indicada da manivela, determine ( a )   a velocidade angular da barra de conexão B D e ( b )   a velocidade do pistão P .

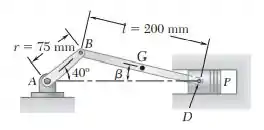
Passo 1

Fala aí, galera. Tudo certo? Bora fazer mais questões de Mecânica pra ficar craque. Sabemos que a manivela A B tem uma velocidade angular horária constante de 1,5 m / s . Assim, expressando a relação entre velocidades v B , v A e v A / B , temos:

v B = v A + v B / A v B ∡ 60 ° = 1,5   m / s   ↓ + [ v B / A ∡ 7 0 ° ]

Com isso, podemos construir um diagrama de vetores na fórmula de um triângulo e assim, utilizar a lei dos senos para determinar as velocidades. Temos:

v B sin ⁡ 7 0 ° = v B / A sin ⁡ 60 ° = 1 , 5   m / s sin ⁡ 5 0 °

E então, podemos determinar a velocidade do pistão v B utilizando esta relação, excluindo o termo do meio. Temos:

v B sin ⁡ 70 ° = 1,5   m / s sin ⁡ 50 ° v B = 1,84   m / s   ∡ 60 °

Passo 2

Através desta mesma relação, podemos determinar v B / A , mas desta vez, vamos excluir o termo inicial da relação e encontrarmos a velocidade v A / B . Fica assim:

v B / A sin ⁡ 60 ° = 1,5   m / s sin ⁡ 50 °

v B / A = 1,696   m / s   ∡   7 0 °

E então, sabemos que podemos encontrar a velocidade angular através da seguinte relação:

v B / A = A B ω A B 1,696   m / s = 0,75 ω A B ω A B = - 2,26   r a d / s

Isso é tudo, pessoal. Bora praticar mais!

Resposta

v B = 1,84   m / s   ∡ 60 °

ω A B = - 2,26   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando um corpo submerso se move em um fluido, as partículas deste fluido circulam em torno do corpo e adquirem energia cinética. No caso de uma esfera movendo-se em um fluido ideal, a energia cinétic
duas hastes uniformes AB e CD, cada uma com comprimento l e massa m, são fixadas às engrenagens conforme mostrado. Sabendo que a massa da engrenagem C está dentro e que a massa da engrenagem A é de 4m
Quatro barras de mesma massa m e comprimento igual a l são conectadas por pinos em A, B, C e D e podem se mover em um plano horizontal. As barras são fixadas a quatro molas de mesma constante k e estã
Três hastes idênticas são conectadas conforme mostrado. Se b = 3 4 l , determine a frequência de pequenas oscilações do sistema.
Uma placa fina de comprimento l repousa sobre um semicilindro deraio r. Deduza uma expressão para o período de pequenas oscilaçõesda p.