Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 58
Uma força atua ao longo da linha . Determine o sistema força-binário equivalente no ponto .
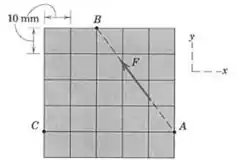
Passo 1
O primeiro passo é escrever uma expressão para a força , já temos o seu módulo, e podemos usar o quadriculado para definir uma direção:
O que fizemos aqui foi multiplicar o módulo pelo vetor unitário que aponta na direção .
O nosso sistema força binário é formado por essa força aplicada ao ponto e o momento dessa força em relação a na sua posição original.
Como um vetor pode ser transladado (deslocado) sem problemas de um ponto para o outro, só falta encontrar o momento.
Passo 2
Então agora só precisamos calcular o momento da força em relação ao ponto , vamos fazer um desenho:
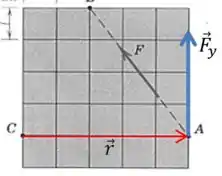
E nós já calculamos a componente vertical de , então o momento da força em relação ao ponto é:
Já que cada quadrado mede .
E é importante dizer que esse momento favorece a rotação no sentido anti-horário.
Resposta
O sistema força binário equivalente é e no sentido anti-horário.