Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 87
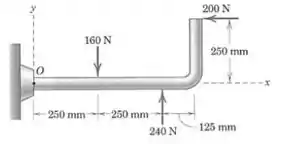
Substitua as três forças atuando no tubo dobrado por uma única força equivalente . Determine a distância a partir do ponto até o ponto no eixo pelo qual passa a linha de ação de .
Passo 1
Vamos começar calculando a força resultante:
E o momento total das forças em relação a , considerando o sentido anti-horário como o positivo para a rotação:
Passo 2
E a força resultante sobre esse tubo deve agir em um ponto que gere o mesmo momento que tínhamos inicialmente.
Como nosso vetor tem componentes nas duas direções vamos fazer um desenho para entender onde está a distância que queremos calcular:
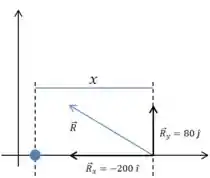
E então:
Resposta
A força resultante é aplicada em .
Exercícios de Livros Relacionados
O suporte está soldado a ponto à extremidade do eixo no ponto O . Para mostrar o efeito da força de 900N sobre a solda, substitua a força por seu equivalente formado por uma força e um binário M → em
O sistema força-binário indicado está aplicado a um pequeno eixo localizado no centro da placa. Substitua esse sistema por uma única força e especifique a coordenada do ponto sobre o eixo x através do
Cada hélice de um navio de duas hélices desenvolve um empuxo de 300k N na velocidade máxima. Ao manobrar o navio, uma hélice está girando a toda velocidade para frente e a outra a toda velocidade no s
Substitua a força de 10k N atuando sobre a coluna de aço por um sistema força-binário equivalente no ponto O . Essa substituição é frequentemente feita no projeto de estruturas.
Uma chave de roda é usada para apertar um parafuso de cabeça quadrada. Se forças de 250N forem aplicadas à chave, como mostrado, determine o módulo F das forças iguais exercidas nos quatro pontos de c